
Rozkład liczb na czynniki pierwsze
Każda liczba naturalna złożona większa od 2 może być przedstawiona jako iloczyn liczb pierwszych.
Rozkład liczb na czynniki pierwsze nazywamy faktoryzacją. Najczęściej do tego celu używamy metody brute force, dzieląc liczbę przez kolejne liczby pierwsze. Faktoryzacja liczb składających się z 300 lub więcej cyfr, jest praktycznie niewykonalna, nawet przy użyciu najszybszych komputerów.
Trudności faktoryzacji dużych liczb są podstawą niezawodności systemów kryptograficznych.
Algorytm faktoryzacji
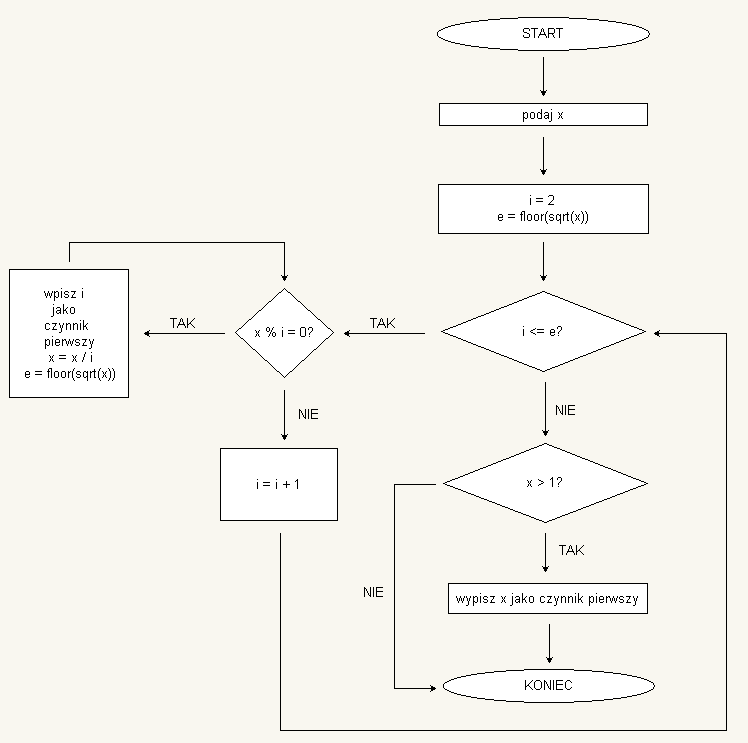
Przykład
![]()
Aby ułatwić odczytanie liczby, powtarzające się liczby zapisujemy w postaci odpowiedniej potęgi tej liczby:
![]()
Właściwości
Jeśli liczba naturalna n ma dwa czynniki pierwsze, to przynajmniej jeden z nich jest mniejszy od
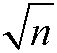
Jeśli czynników pierwszych jest m to przynajmniej jeden jest mniejszy niż
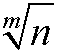
Zastosowania
- Obliczanie największego wspólnego dzielnika (nwd)
- Obliczanie najmniejszej wspólnej wielokrotności (nww)
- Systemy kryptograficzne
Linki
Wykaz czynników pierwszych liczb od n=2 do n=1000

