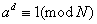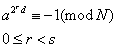Liczby pierwsze

Liczby pierwsze

Pojęcie liczby pierwszej

Liczby pierwsze znane są od wieków i przez wieki były przedmiotem dociekań wielu matematyków, co świadczy o skali problemu. Liczby pierwsze byłyby jednak do dziś matematyczną ciekawostką do dręczenia studentów matematyki, gdyby nie fakt, że znalazły intensywne zastosowanie w kryptografii.

Liczba pierwsza to taka liczba, która jest większa od 1 i jej jedynymi dzielnikami są 1 i ona sama.

2 jest liczbą pierwszą bo dzieli się tylko przez 1 i 2. 3 jest liczbą pierwszą gdyż dzieli się jedynie przez 1 i 3. 4 nie jest liczbą pierwszą bo dzieli się przez 1,2 i 4.

Każda liczba naturalna większa od 2, która nie jest liczbą pierwszą jest liczbą złożoną.

0 nie jest ani liczbą pierwszą ani liczbą złożoną.

1 nie jest ani liczbą pierwszą ani liczbą złożoną.

Zbiór liczb pierwszych oznacza się znakiem ℙ.

Rozmieszczenie liczb pierwszych

A oto liczby pierwsze w zakresie od 2 do 1000

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73,
79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163,
167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251,
257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443,
449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557,
563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647,
653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757,
761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863,
877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983,
991, 997

Jest ich 168.

Rozmieszczenie liczb pierwszych w zakresie od n = 1 do n = 10000

Jak do tej pory nikt nie znalazł wzoru określającego dokładne rozmieszczenie liczb pierwszych wśród liczb naturalnych.

Spirala Ulama

W 1963 r. Stanisław Ulam – polski matematyk – wypisał liczby pierwsze na spirali kwadratowej. Na niektórych przekątnych liczby pierwsze występują częściej niż na innych przekątnych. Fakt ten nie został do tej pory wyjaśniony.

Spirala Archimedesa

Liczby od n = 2 do n = 1000 rozmieszczone na spirali Archimedesa.

Gęstość liczb pierwszych

Udział liczb pierwszych w zakresie od n = 1 do n = 100
000 000

Zakres:	Liczb pierwszych	%	Narastająco	%
1-10	4	40,00	4	40,00
10-100	21	21,00	25	25,00
100-1000	143	14,30	168	16,80
1000-10000	1061	10,61	1229	12,29
10000-100000	8363	8,36	9592	9,59
100000-1000000	68906	6,89	78498	7,85
1000000-10000000	586081	5,86	664579	6,65
10000000-100000000	5096876	5,10	5761455	5,76

Gęstość liczb pierwszych najczęściej określa się jako % stosunek liczb pierwszych do ogólnej liczby liczb w przedziałach zamkniętych od 2 do 2ⁿ, gdzie n jest kolejną liczbą naturalną.

Lp.	Przedział		Liczba liczb pierwszych	%
	a	b
1	2	21	1	100.0
2	2	22	2	66.67
3	2	23	4	57.14
4	2	24	6	40.0
5	2	25	11	35.48
6	2	26	18	28.57
7	2	27	31	24.41
8	2	28	54	21.18
9	2	29	97	18.98
10	2	210	172	16.81
11	2	211	309	15.1
12	2	212	564	13.77
13	2	213	1028	12.55
14	2	214	1900	11.6
15	2	215	3512	10.72
16	2	216	6542	9.98
17	2	217	12251	9.35
18	2	218	23000	8.77
19	2	219	43390	8.28
20	2	220	82025	7.82
21	2	221	155611	7.42
22	2	222	295947	7.06
23	2	223	564163	6.73
24	2	224	1077871	6.42

Twierdzenie Gaussa i hipoteza Riemanna

Oba wzory dotyczą liczby π(n) liczb pierwszych w przedziale od [1, n].

Twierdzenie Gaussa

Gauss uważał, że liczba liczb pierwszych wynosi:

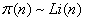
gdzie Li(n) jest resztą logarytmu całkowego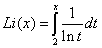

~ oznacza równość asymptotyczną oznaczającą, że:

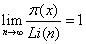
Po rozwinięciu logarytmu całkowego w szereg otrzymujemy:

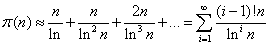
z którego do obliczeń przyjmuje się jedynie pierwszy człon, przy zachowaniu asymptotycznej równości:

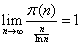
Liczba liczba pierwszych mniejszych od 10000 powinna wynosić:

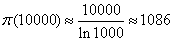
Faktycznie n = 1229

Hipoteza Riemanna

Rieman twierdził, że liczba liczb pierwszych mniejszych od n wynosi:

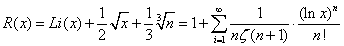
gdzie:

ζ jest funkcją dzeta Riemanna.

Porównanie dokładności

Gdy dokonamy stosownych obliczeń:

Udział liczb pierwszych w zakresie od n = 1 do n = 100
000 000

Zakres do:	Liczba liczb pierwszych
	faktyczna	wg Gaussa	wg Riemanna
100	25	22	30
1000	168	145	178
10000	1229	1086	1246
100000	9592	8686	9630
1000000	78498	72382	78628
10000000	664579	620421	664918
100000000	5761455	5428681	5762209

Liczba liczb pierwszych

Liczb pierwszych jest nieskończenie wiele.

Generowanie liczb pierwszych

Brute force

Bierzemy kolejne liczby n. Każdą z n dzielimy przez wszystkie liczby od 2 do n – 1. Jeśli liczba dzieli się przez jakąkolwiek liczbę – nie jest liczbą pierwszą.

Sito Eratostenesa

Ze zbioru liczb naturalnych wybieramy przedział [2,n).

Pierwszą liczbą pierwszą jest 2. Wykreślamy wszystkie wielokrotności 2, a więc 4, 6, etc.

Przechodzimy do pierwszej niewykreślonej liczby, która jest liczbą pierwszą (nie została wykreślona). W naszym przykładzie jest to 3. Wykreślamy wszystkie wielokrotności tej liczby, np. 3, 9 (6 już zostało wykreślone bo jest podzielne przez 2).

Wykreślanie powtarzamy. Jeżeli wykreślana liczba jest większa od pierwiastka z n (u nas 11 bo pierwiastek a n = 10) – wykreślanie przerywamy.

Niewykreślone liczby z przedziału [2,n) to liczby pierwsze.

Animowane sito Ertostenesa

Sito Atkina

Jest bardzo dokładnie opisane na stronie Wikipedii pod hasłem “Sito Atkina”.

Porównanie sit

Algorytmy napisane były przeze mnie. Czas obejmuje czas wpisania liczb do tablicy i wykreślenia z niej liczb nie będących liczbami pierwszymi. Czas był obliczany na moim komputerze o dość przeciętnych parametrach:

Zakres liczb od 2 do n	Czas w sek
	Sito Eratostenesa	Sito Atkina
1 000 000	0,011	0,020
10 000 000	0,098	0,085
100 000 000	1,807	1,324
1 000 000 000	21,655	15,585

Inne sita

Istnieje kilka innych sit, z których najpopularniejsze jest sito Sundarama.

Liczby pierwsze Mersenne’a

Liczby Mersenne’a to liczby typu:

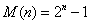
Liczby pierwsze Mersenne’a to liczby Mersenne’a, które są zarazem liczbami pierwszymi.

Jeżeli liczba n w 2ⁿ jest złożona, to M(n) nigdy nie jest liczbą pierwszą.

Jeżeli liczba n w 2ⁿ jest pierwsza to M(n) może być liczbą pierwszą.

Aby przekonać się, że liczba jest pierwsza należy wykonać odpowiedni test pierwszości. Najczęściej używa się testu Lucasa – Lehmera.

Większość największych znanych liczb pierwszych to liczby Mersenne’a.

Znamy 49 liczb pierwszych Mersenne’a.

25 liczb pierwszych Mersenne’a

Wzór Fermata i inne wzory

Liczby Fermata

Liczby pierwsze Fermata to liczby obliczane według wzoru:

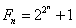
które są pierwsze.

Na razie znamy 4 liczby Fermata:

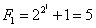
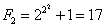
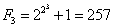
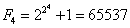
Niestety liczba F₅:

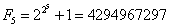
nie jest liczbą pierwszą podobnie jak F₆.

n² – n + 41

Dla liczb od n = 1 do n = 40 wyrażenie daje liczby pierwsze. Natomiast dla n = 41 otrzymujemy liczbę złożoną (412)

Liczby pierwsze Eulera

Są to liczby postaci:

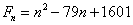
Wzór generuje liczby pierwsze od n = 1 do n = 79. Zawodzi niestety przy n = 80

Specjalne liczby pierwsze

Liczby pierwsze bliźniacze

Liczby bliźniacze to dwie liczby pierwsze różniące się o 2.

• (3, 5)
• (5, 7)
• (11, 13)
• (17, 19)
• (29, 31)
• (41, 43)
• (59, 61)
• (71, 73)
• …
• (1619, 1621)
• …

Wszystkie liczby bliźniacze od 2 do 100 000:

Liczby pierwsze czworacze

Liczby czworacze to cztery liczby pierwsze różniące się od p o 2, 6 i 8, czyli równe p, p+ 2, p+6, p + 8:

• (5, 7, 11, 13)
• (101, 103, 107, 109)
• (821, 823, 827, 829)

Wszystkie liczby czworacze od 2 do 100 000:

Liczby pierwsze izolowane

Liczba pierwsza p jest izolowana, jeśli najbliższa liczba pierwsza różni się od niej co najmniej o 4.

• 89, 157, 173

Wszystkie liczby izolowane od 2 do 1000:

Liczby pierwsze Sophie Germain

Liczba pierwsza jest liczbą Sophie Germain, jeśli liczba 2p+ 1 także jest liczbą pierwszą.

• 2 (3)
• 3 (7)
• 5 (11)
• 11 (23)
• 23 (47)
• 29 (59)
• 41 (83)
• 53 (107)
• 83 (167)

Wszystkie liczby Sophie Germain od 2 do 10000:

Liczby pierwsze lustrzane

Liczby pierwsze lustrzane to dwie liczy, z których druga ma odwrotną kolejność cyfr dziesiętnych niż pierwsza.

• 13 i 31
• 17 i 71
• 37 i 73
• 79 i 97
• 107 i 701

Wszystkie liczby lustrzane od 1 do 10000:

Liczby palindromiczne

Są to liczby, które po zapisaniu ich cyfr dziesiętnych w odwrotnej kolejności pozostają tymi samymi liczbami

• 11
• 101
• 131
• 191
• 929

Wszystkie liczby palindromiczne od 1 do 100000:

Największe liczby pierwsze

Największą znaną liczbą pierwszą sprzed epoki komputerów była 44-cyfrowa liczba Ferriera =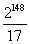

20988936657440586486151264256610222593863921

Liczba ma 44 cyfry.

Największą znaną liczbą pierwszą, która nie jest liczbą Mersenne’a jest:

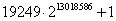
W zapisie 10-nym liczy 3918990 (2177 stron maszynopisu). Jest 11 na liście największych liczb pierwszych.

Dziesięć największych znanych cyfr to liczby pierwsze Mersenne’a (stan na styczeń 2013)

Poprzednią największą znaną liczbą pierwszą to 48 liczba Mersenne’a:

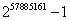
Składa się z 17425170 cyfr dziesiętnych (9681 stron maszynopisu). Została odkryta 25 stycznia 2013 r.

Największą znaną liczbą pierwszą jest 49 liczba Mersenne’a znaleziona przez Curtisa Coopera z Uniwersytetu w Missouri:

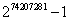
Składa się z 22 338 618 cyfr (12 411 stron maszynopisu). Doniesienie pojawiło się w dn. 21.01.2016.

Testy pierwszości

Testy pierwszości to testy pozwalające określić czy dana liczba jest liczbą pierwszą.

Dzielenie

Oczywiście najprostszą metodą jest próba dzielenia liczby. Metoda zawodzi przy dużych liczbach, ze względu na czas potrzebny do wykonania dzieleń.

Sito Erastotenesa i Atkina

Jeśli liczba pozostanie na sicie – jest liczbą pierwszą. Ta metoda zawodzi przy bardzo dużych n, ale ze względu na prostotę jest często wykorzystywana.

Test Millera – Rabina

Przy dużych liczbach praktyczne zastosowanie mają testy probabilistyczne, które pozwalają, z dostatecznie dużym prawdopodobieństwem, określić czy liczba jest liczbą pierwszą.

Do badania pierwszości dużych liczb najczęściej stosuje się test Millera – Rabina., który w odpowiedzi daje true albo false. False oznacza, że liczba z całą pewnością nie jest pierwsza. Odpowiedź true znaczy, że liczba ta jest z dużym prawdopodobieństwem liczbą pierwszą. Im większa liczba iteracji algorytmu tym większe prawdopodobieństwo, że badana liczba jest liczbą pierwszą.

Test Millera – Rabina wykorzystuje arytmetykę modularną.

Postępowanie

1. Wybierz k ≥ małych liczb a < N i względnie pierwszych z N.
2. Zapisz N – 1 w postaci 2^sd
3. Sprawdzaj, czy zachodzi któryś z warunków
   • 
   • 
4. Jeśli, dla pewnego a nie zaszedł któryś z powyższych warunków, to N jest złożone. W przeciwnym wypadku uważaj N za pierwsze, z prawdopodobieństwem błędu (1/4)^k

Test nie daje pewności, że badana liczba jest pierwsza, ale przy odpowiednio dużym k można się do pewności zbliżyć.

Przykład

Sprawdzamy, czy liczba 577 jest pierwsza.

Mamy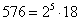

Przyjmujemy a=2

Mamy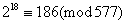

dla k = 1

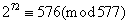dla k = 2

a = 2 spełnia więc jeden z warunków

Przyjmujemy teraz a = 3

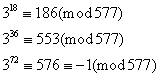
Liczba a = 3 również spełnia warunki testu. Zatem z prawdopodobieństwem:

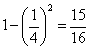
577 jest liczbą pierwszą

Test Lucasa – Lehmera

Często używa się testu Lucasa – Lehmera, również opartego na arytmetyce modularnej.

Test służy do badania pierwszości liczb Mersenne’a.

Można wykazać, że la nieparzystych p liczba 2^p – 1 jest liczbą pierwszą wtedy i tylko wtedy, gdy 2^p – 1 dzieli S(p – 1). Funkcja S(k) jest określona rekurencyjnie jako:

S(1) = 4 oraz S(n+1) = S(n)² – 2

Przykład

Badamy p = 5, 2⁵ – 1 = 31

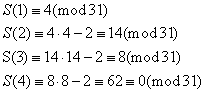
A zatem 31 jest liczbą pierwszą.

Przykład

Badamy p = 9, 2⁹ – 1 = 511

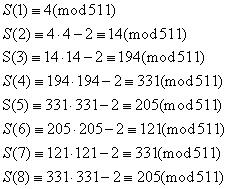
A zatem 511 nie jest liczbą pierwszą.

Inne testy

Istnieje mnóstwo testów pierwszości, łatwych do znalezienia w Internecie.

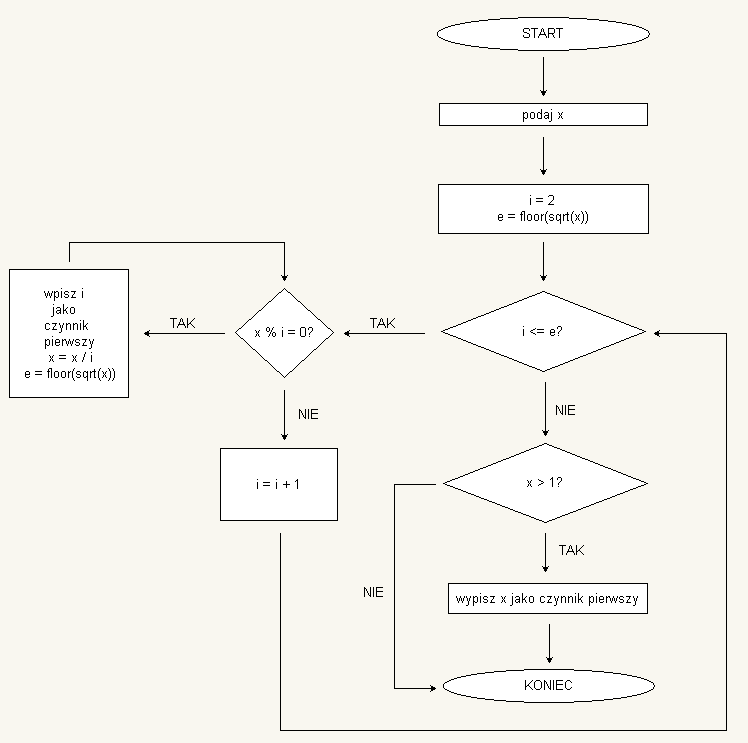
Faktoryzacja

Każda liczba złożona większa od 2 może być przedstawiona w postaci iloczynu liczb pierwszych.

Np. liczba 100010001000 = 2*2*2*3*5*5*5*7*13*37*9901

Aby ułatwić odczytanie liczby powtarzające się liczby zapisujemy w postaci odpowiedniej potęgi tej liczby:

Np. liczba 100010001000 = 2³*3*5³*7*13*37*9901

Rozkład liczb od n = 2 do n = 1000 na czynniki pierwsze

Schemat algorytmu faktoryzacji:

Ciekawe liczby pierwsze

Liczba 11111111111111111111111 (23 jedynki) też jest liczbą pierwszą.

Liczba 31415926535897932384626433832795028841 złożona z pierwszych 38 cyfr liczby π – jest liczbą pierwszą.

Liczba 73939133 jest liczbą pierwszą. Gdy odetniemy jej kolejno po 1 cyfrze z prawej strony:

• 739391
• 73939
• 7393
• 739
• 73
• 7

to każda z powstałych liczb jest liczbą pierwszą.

Czego nie wiadomo?

• Formuła rozkładu liczb pierwszych wśród liczb naturalnych.
• Czy dla każdego n > 0 w przedziale między n², a (n + 1)² istnieje liczba pierwsza?
• Czy każda liczba parzysta jest sumą dwóch liczb pierwszych?
• Czy istnieje nieskończenie wiele liczb pierwszych bliźniaczych, Fermata, Mersenne’a, Germain?
• Czy istnieje nieskończenie wiele liczb pierwszych postaci n² + 1?
• Czy ciąg Fibonacciego zawiera nieskończenie wiele liczb pierwszych?

Zastosowania

Zastosowania praktyczne

Liczby pierwsze są stosowane głównie w kryptografii do tworzenia podpisów cyfrowych np. w algorytmach typu RSA. Trudność złamania szyfru i odgadnięcia klucza polega na trudności związanej z faktoryzacją liczby, która jest iloczynem 2 bardzo dużych liczb pierwszych.

Liczby pierwsze w naturze

Cykady z rodzaju Magicicada większość czasu spędzają w postaci larwalnej pod ziemią. Na wiosnę wychodzą z ziemi, przobrażają się, odlatują, rozmnażają, składają jaja zamykając w ten sposób cykl życiowy.

Istnieją gatunki, u których cykl życiowy jest wstrzymywany na 7, 13 albo nawet 17 lat, czyli larwy pojawiają się i przeobrażają jedynie co 7, 13 albo 17 lat.

Prawdopodobnie jest to zabezpieczenie przed koewolucją drapieżców i pasożytów, zjadających lub atakujących cykady. Drapieżce i pasożyty mają problemy z odpowiednią synchronizacją swoich cykli życiowych z cyklem życia cykad. Im okres cyklu jednego gatunku jest większą liczbą pierwszą tym trudniejsza synchronizacja.

Copyright Jacek Piechota, Opublikowano 9 stycznia 2016