Trójkąt Pascala
Jeżeli pominiemy x-y i y-ki to współczynniki liczbowe rozwinięć kolejnych potęg dwumianu Newtona możemy zapisać w postaci tzw. trójkąta Pascala:
Właściwości
Właściwość 1
Liczby stojące w n-tym wierszu to rozwinięcia dwumianu Newtona dla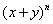 
.
Wiersz piąty (wiersze są liczone od 0) to rozwinięcie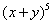 
= 1,5,10,10,5,1
Właściwość 2
Suma wyrazów w linii dla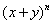 
wynosi 
.
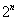Np. suma wyrazów dla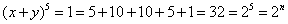 
Właściwość 3
Dany wyraz jest sumą dwu wyrazów stojących bezpośrednio powyżej niego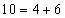 
:
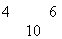
Właściwość 4
Liczba stojąca na miejscu (liczonym od zera) k w wierszu (liczonym od zera) n jest równa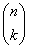 
Np. w wierszu 5 na miejscu 2 stoi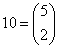 
Właściwość 5
Na skrajnych bokach trójkąta są same jedynki:
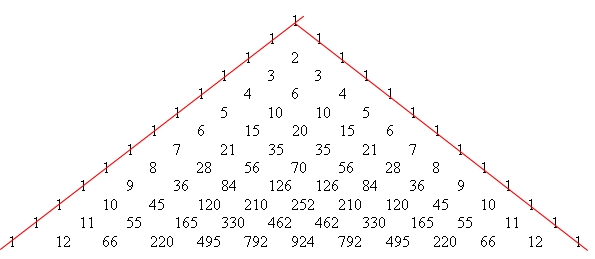
Właściwość 6
Na bardziej wewnętrznych bokach trójkąta ułożone są liczby naturalne:
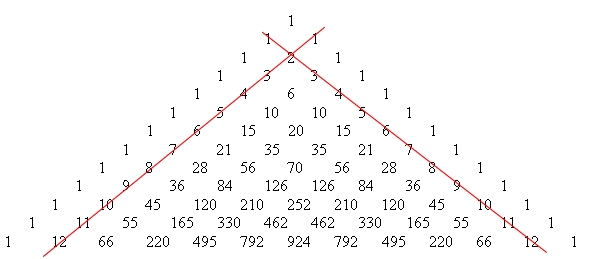
Właściwość 7
Jeszcze bardziej wewnętrzne boki zawiera liczby trójkątne. Liczba trójkątna podaje liczbę okręgów przy układaniu w kształt trójkąta:
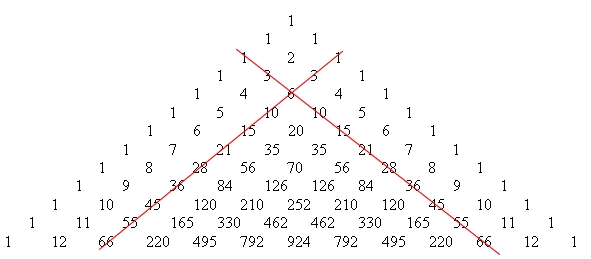
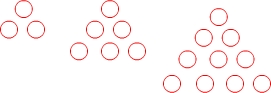
Właściwość 8
Na jeszcze bardziej wewnętrznych bokach występują liczby piramidalne. Liczba piramidalna to liczba kulek ułożonych w czworościan foremny.
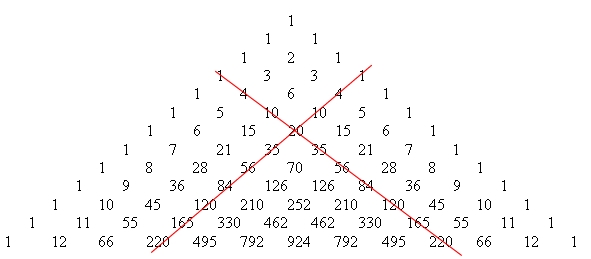
Właściwość 9
Każda liczba określa liczbę dróg jakimi można do niej dotrzeć od wierzchołka trójkąta, przy założeniu, że poruszamy się wyłącznie w ‘lewo dół’ lub w ‘prawo dół’.
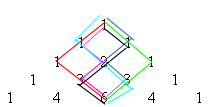
Właściwość 10
Suma kwadratów wszystkich elementów wiersza (liczonych od zera) n jest równa środkowemu elementowi wiersza 2n.
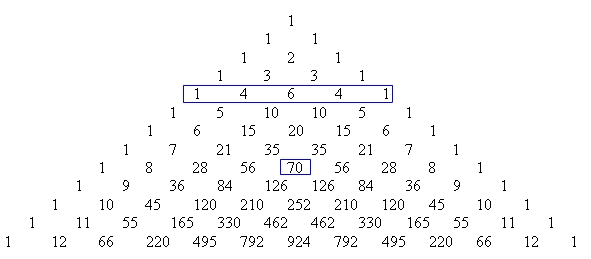
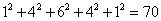
Właściwość 11
Po usunięciu z trójkąta Pascal np. liczb parzystych pozostałe liczby tworzą kształt trójkąta Sierpińskiego. Podobna prawidłowość dotyczy także dowolnych liczb naturalnych, np. przez wykreślenie liczb niepodzielnych przez 3.
| 1 |
| 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 3 | 1 |
| 1 | 4 | 6 | 4 | 1 |
| 1 | 5 | 10 | 10 | 5 | 1 |
| 1 | 6 | 15 | 20 | 15 | 6 | 1 |
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 |
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
| 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 |
| 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 |
| 1 | 13 | 78 | 286 | 715 | 1287 | 1716 | 1716 | 1287 | 715 | 286 | 78 | 13 | 1 |
| 1 | 14 | 91 | 364 | 1001 | 2002 | 3003 | 3432 | 3003 | 2002 | 1001 | 364 | 91 | 14 | 1 |
| 1 | 15 | 105 | 455 | 1365 | 3003 | 5005 | 6435 | 6435 | 5005 | 3003 | 1365 | 455 | 105 | 15 | 1 |
| 1 | 16 | 120 | 560 | 1820 | 4368 | 8008 | 11440 | 12870 | 11440 | 8008 | 4368 | 1820 | 560 | 120 | 16 | 1 |
| 1 | 17 | 136 | 680 | 2380 | 6188 | 12376 | 19448 | 24310 | 24310 | 19448 | 12376 | 6188 | 2380 | 680 | 136 | 17 | 1 |
Właściwość 12
Jeżeli zsumujemy liczby w kolejnych równoległych liniach jak pokazano na rysunku otrzymamy kolejne liczby Fibonacciego.
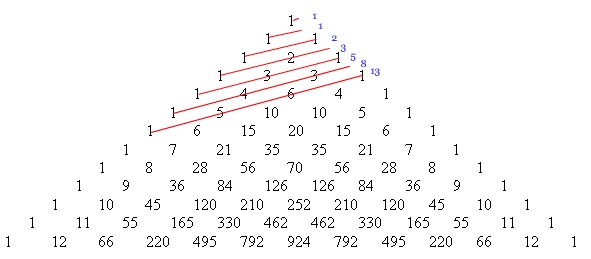
Wyrazy ciągu Fibonacciego można obliczyć używając symbolu Newtona jako:
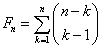
gdzie:
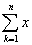oznacza sumę x-ów od k = 1 do k = n.
Obliczymy 5 wyraz ciągu Fibonacciego:
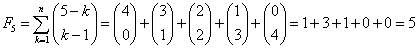
Obliczymy 6 wyraz ciągu Fibonnaciego:
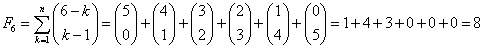
Przykłady
Przykład 1
W większości przypadków niepotrzebne są nam pełne rozwinięcia, a jedynie współczynniki. Obliczymy współczynniki dla 5 i 20 rzędu trójkąta Pascala.
A oto wynik:
n = 5 [1, 5, 10, 10, 5, 1] n = 20 [1, 20, 190, 1140, 4845, 15504, 38760, 77520, 125970, 167960, 184756, 167960, 125970, 77520, 38760, 15504, 4845, 1140, 190, 20, 1]
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.