
Największy wspólny dzielnik (nwd)
Definicja
Największy wspólny dzielnik liczb a i b to największa liczba, która jest dzielnikiem zarówno a jak i b.
Największym wspólnym dzielnikiem liczb 1350 i 325 jest 25.
Największy wspólny dzielnik oznaczamy nwd albo nwd(a, b).
nwd(1350, 325)=25
Obliczanie przez wyznaczenie dzielników
Przykład 1
Liczba a = 16 ma dzielniki: 1, 2, 4, 8, 16
Liczba b = 14 ma dzielniki: 1, 2, 3, 7, 14
Jak widzimy największą liczbą, która jest zarówno dzielnikiem a jak i b jest liczba 2.
Oznaczamy nwd(16, 14) = 2
Przykład 2
Liczba a = 45 ma dzielniki: 1, 3, 5, 9, 15, 45
Liczba b = 30 ma dzielniki: 1, 2, 3, 5, 6, 10, 15, 30
Jak widzimy największą liczbą, która jest zarówno dzielnikiem a jak i b jest 15.
Zapisujemy nwd(45, 30) = 15.
Obliczanie przy użyciu algorytmu Euklidesa
Dla liczb a i b największy wspólny dzielnik obliczamy następująco:
- dzielimy a przez b i znajdujemy resztę r1
- Jeśli reszta r1 nie jest równa 0 dzielimy b przez r1 i dostajemy resztę r2
- Jeśli reszta r2 nie jest równa 0, dzielimy r1 przez r2 i znajdujemy resztę r3
- Obliczenia powtarzamy do otrzymania pierwszej reszty równej 0
- Ostatnia niezerowa reszta to nwd(a, b)
Przykład 1
Liczba a = 16
Liczba b = 14
Dzielimy a:b = 16:14 = 1 r1 = 2
Dzielimy b:r1 = 14:2 = 7 r2 = 0
- nwd(16, 14)=2
Przykład 2
Liczba a = 45
Liczba b = 30
Dzielimy a:b = 45:30 = 1 r1 = 15
Dzielimy b:r1 = 30:15 = 2 r2 = 0
- nwd(45, 30)=15
Przykład 3
Liczba a = 1345
Liczba b = 325
Dzielimy a:b = 1345:325 = 4 r1 = 45
Dzielimy b:r1 = 325:45 = 7 r2 = 10
Dzielimy r1:r2 = 45:10 = 4 r3 = 5
Dzielimy r2:r3 = 10:5 = 2 r4 = 0
- nwd(1345, 325)=5
Obliczanie przez rozkład na czynniki pierwsze
Największy wspólny dzielnik jest iloczynem czynników pierwszych występujących w rozkładzie obu liczb.
Przykład 1
Liczba a = 56 = 2⋅2⋅2⋅7
Liczba b = 42 = 2⋅3⋅7
- nwd(56, 14) = 2⋅7 = 14
Przykład 2
Liczba a = 45 = 3⋅3⋅5
Liczba b = 30 = 2⋅3⋅5
- nwd(45, 30) = 3⋅5 = 15
Obliczanie dla trzech i więcej liczb
nwd możemy obliczyć dla trzech liczb biorąc pod uwagę, że:
![]()
Przykład
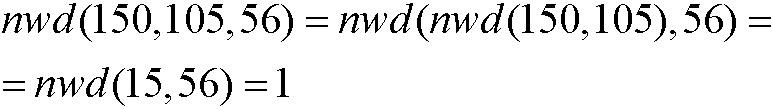
Przez analogię możemy obliczyć największy wspólny dzielnik dla dowolnej liczby liczb.
Obliczanie z najmniejszej wspólnej wielokrotności (nww)
Ponieważ
![]()
więc
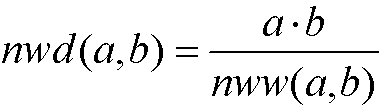
Prawdziwa jest też zależność
![]()
Zastosowania
Największy wspólny dzielnik (nwd) jest wykorzystywany do:
- Obliczania najmniejszej wspólnej wielokrotności (nww)
- Sprawdzania, czy liczby są względnie pierwsze
- Sprowadzania (redukcji) ułamków do postaci nieskracalnej
Terminy powiązane
- Najmniejsza wspólna wielokrotność (nww)
- Liczby względnie pierwsze
- Rozkład liczb na czynniki pierwsze
- Sprowadzanie (redukcja) ułamków do postaci nieskracalnej

