Zastosowania wzorów Bernoulliego
I prawo Mendla
Rozszczepienie genotypów przy dziedziczeniu jednej cechy:
Przy niepełnym dominowaniu
Otrzymujemy rozszczepienie genotypów i fenotypów 1:2:1 (czerwony : różowy : biały)
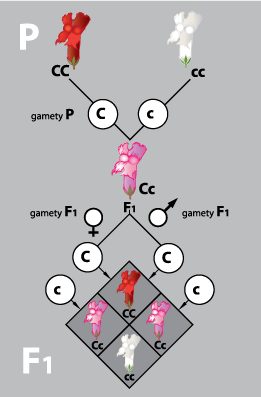
Przy pełnym dominowaniu
Otrzymujemy rozszczepienie genotypów 1:2:1 i rozszczepienie fenotypów 3:1 (czerwony: biały)
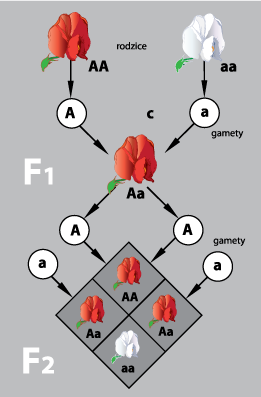
Obliczenie prawdopodobieństwa zachorowania potomstwa
Np. jeżeli mamy troje dzieci użyjemy trzeciego rzędu trójkąta Pascala:
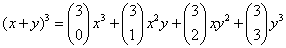
Jeżeli dzieci mogą zachorować na pewną chorobę to mamy:
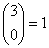możliwość, że wśród trojga dzieci 0 będzie chorych:
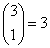możliwości, że wśród trojga dzieci 1 będzie chore,
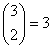możliwości, że wśród trojga dzieci 2 będzie chorych,
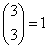możliwość, że wśród trojga dzieci 3 będzie chorych.
Ponieważ suma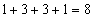 
możemy łatwo obliczyć prawdopodobieństwa poszczególnych zdarzeń. Wynoszą one odpowiednio 
.
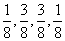Powyższe wyliczenie jest słuszne jeśli prawdopodobieństwo zdrowia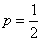 
i prawdopodobieństwo choroby 
.
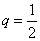Jeżeli np. z powodów genetycznych prawdopodobieństwa zdrowia i choroby są różne to należy użyć innego wzoru albo obliczyć to następująco:
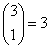oznacza troje dzieci: 1 jest chore, dwoje jest zdrowych.
Jeżeli prawdopodobieństwo choroby wynosi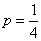 
, a zdrowia 
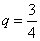to obliczenie będzie następujące:
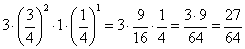
Prawdopodobieństwo, że dwoje dzieci jest zdrowych, a 1 jest chore wynosi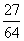 
Zauważ, że suma wykładników potęgowych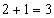 
Obliczanie częstości genów
Prawo Hardy’ego – Weinberga, to podstawowe prawo genetyki populacyjnej stwierdzające, że w populacjach (spełniających pewne warunki) częstość poszczególnych genotypów nie zmienia się z pokolenia na pokolenie.
Przy cesze reprezentowanej przez dwa allele A i a jednego genu, rozkład genotypów jest określony równaniem:
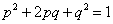
gdzie:
p i q to częstości (prawdopodobieństwa napotkania) alleli A i a.
pp to częstość homozygot dominujących AA, pq to prawdopodobieństwo heterozygot Aa, a qq to prawdopodobieństwo homozygot recesywnych aa.