Prawdopodobieństwo wyrzucenia
Zgodnie z wzorem na rzut n monetami, jeżeli jakieś zdarzenie występuje z prawdopodobieństwem p w każdej z n niezależnych prób, to prawdopodobieństwo, że w danej próbie zdarzenie wystąpi k razy (k < n) wynosi:
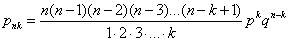
gdzie q jest prawdopodobieństwem nie wystąpienia zdarzenia.
Jeżeli rzucimy jednocześnie np. 4 monetami to prawdopodobieństwo wyrzucenia 4 orłów zgodnie z powyższym wzorem:
n = 4, k = 4
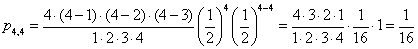
Jeżeli rzucimy jednocześnie np. 4 monetami to prawdopodobieństwo wyrzucenia 3 orłów zgodnie z powyższym wzorem:
n = 4, k = 3
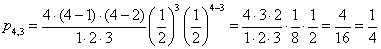
Jeżeli rzucimy jednocześnie np. 4 monetami to prawdopodobieństwo wyrzucenia 2 orłów zgodnie z powyższym wzorem:
n = 4, k = 2
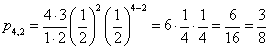
Jeżeli rzucimy jednocześnie np. 4 monetami to prawdopodobieństwo wyrzucenia 1 orła zgodnie z powyższym wzorem:
n = 4, k = 1
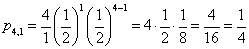
Jeżeli rzucimy jednocześnie np. 4 monetami to prawdopodobieństwo wyrzucenia 0 orłów zgodnie z powyższym wzorem:
n = 4, k = 0
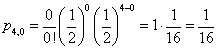
Jak widzimy można by to obliczyć prościej.
Gdy rzucamy jednocześnie n monetami i liczymy prawdopodobieństwo k sukcesów (wyrzucenia np. orłów) to prawdopodobieństwo wynosi:
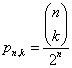
Np. dla n = 4, i k = 3
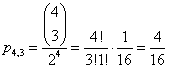
Gdybyśmy rzucali 400 razy 4 monetami i chcielibyśmy wiedzieć ile razy wyrzucimy 4 orły to oczywiście obliczone prawdopodobieństwo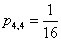 
musielibyśmy pomnożyć przez liczbę rzutów 
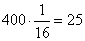. W 400 próbach polegających na rzucie 4 monetami możemy spodziewać się, że cztery orły otrzymamy 25 razy.
Zwróćmy uwagę, że wzór
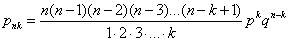
jest ogólny. Prawdopodobieństwa wcale nie muszą być równe. Jeżeli rzucamy kostką do gry to prawdopodobieństwo wyrzucenia '1′ jest równe 1/6, a prawdopodobieństwo zdarzenia przeciwnego (nie wyrzucenia '1′) wynosi '5/6′
Np. rzucamy 5 kostkami jednocześnie. Jakie jest prawdopodobieństwo wyrzucenia dwóch '6′ w danej próbie?
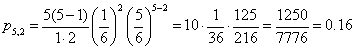
Wzór Bernoulliego
Jeżeli przyjrzymy się uważniej to powyższy wzór możemy uprościć:
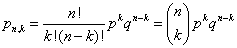
gdzie
p to prawdopodobieństwo sukcesu
q to prawdopodobieństwo porażki
n to liczba zdarzeń
k to liczba zdarzeń sprzyjających
Przykłady
Przykład 1
Sprawdzamy nasze obliczenia. Obliczamy:
1. prawdopodobieństwo wyrzucenia 3 orłów przy rzucie 4 monetami jednocześnie
2. Prawdopodobieństwo wyrzucenia dwóch '6′ przy rzucie pięcioma kostkami do gry jednocześnie.
Otrzymujemy w wyniku:
0.2500 0.1607420267283988477794240
co potwierdza nasze wyliczenia.
Przykład 2
Jak widzimy już przy prowadzaniu danych musieliśmy zaokrąglić prawdopodobieństwa i wynik jest mało czytelny i niedokładny. Dlatego konieczne jest wprowadzenie nowej klasy Fraction (ułamek) służącej do liczenia wyłącznie w ułamkach. Oczywiście stosowna metoda przelicznikowa pozwala na podanie ostatecznego wyniku w liczbie dziesiętnej. Ale jest to jedyne zaokrąglenie w trakcie obliczeń. Klasa Fraction zamienia również ułamki dziesiętne na normalne, podobnie jak ułamki okresowe na normalne.
Obliczamy:
1. prawdopodobieństwo dla n = 3, k = 4 przy prawdopodobieństwach p i q = 0.5
2. To samo z użyciem klasy Fraction.
3. prawdopodobieństwo dla n = 5, k = 2 przy prawdopodobieństwach p = '0.16666′(1/6) i q = '0.83334′ (5/6)
4. To samo ale przy użyciu klasy Fraction i ułamków normalnych.
A oto wynik:
1: 0.2500 2: [1, 4] (kolejno licznik i mianownik ułamka) 3: 0.1607420267283988477794240 4: [625, 3888] (kolejno liczni i mianownik ułamka) 4: (po podzieleniu 625/3888) 0.1607510288065843621399177
Otrzymujemy nieco inną i dokładniejszą liczbę. Ta dokładność jest szczególnie ważna przy mnożeniu prawdopodobieństw, które na ogół są małymi lub bardzo małymi ułamkami.
Przykład 3
Jakie jest prawdopodobieństwo, że wśród 10 spotkanych na ulicy osób dokładnie dwie osoby będą miały
oczy niebieskie. Kolejność nie ma znaczenia. Wiadomo, że rozkład kolorów oczu jest następujący:
- niebieskie – 7%
- zielone – 1%
- brązowe – 90%
- szare – 2 %
Liczba doświadczeń n = 10
Liczba zdarzeń sprzyjających k = 2
Prawdopodobieństwo sukcesu p = 0.07
Prawdopodobieństwo porażki q = 1 – 0.07 = 0.93
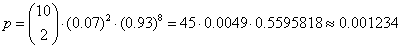
Przykład 4
Dla danych z przykładu 3. Jakie jest prawdopodobieństwo spotkania dwu lub więcej osób
o oczach niebieskich.
Zadanie można rozwiązać na 2 sposoby:
- Zsumować obliczone oddzielnie prawdopodobieństwa spotkania 2, 3, 4, 5, 6, 7, 8, 9, 10 osób
- Zsumować obliczone oddzielnie prawdopodobieństwa spotkania 0 lub 1 osoby i odjąć od 1
Ta druga metoda wymaga mniejszej liczby obliczeń.
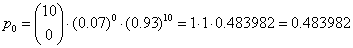
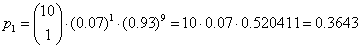
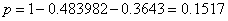
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.