System sześćdziesiętny (2)

System sześćdziesiętny (2)

Poprzednia część artykułu

Tablice kwadratów i sześcianów

W 1854 r. w Senkerah nad Eufratem znaleziono dwie tabliczki z ok. 2000 r. p.n.e. zawierające kwadraty liczb od 1 do 59 oraz sześciany liczb od 1 do 32

Załóżmy, że mamy odpowiednią tabliczkę kwadratów:

5² = [25] = 25;

41² = [28,1] = 1681;

Mamy do pomnożenia 23 x 18 =?

Używamy algorytmu ab=[(a+b)² – (a-b)²]/4 czyli

23 x 18 = [(23+18)² – (23-18)²]/4 czyli

	18	*	23	=	?
	+		–
	23		18
	=		=
	41		5
kwadrat	1681	–	25	=	1656
				/	4
				=	414

czyli;

		*		=	[?]
	+		–
	=		=
kwadrat		–		=
				/
				=

czyli

	[18]	*	[23]	=	[?]
	+		–
	[23]		[18]
	=		=
	[41]		[5]
kwadrat	[28;1]	–	[25]	=	[27;36]
				/	[4]
				=	[6;54]

Innym algorytmem było:

ab = [(a+b)² – a² – b²]/2

Ułamki

Ułamki były znane już wcześniej, ale dopiero zastosowanie zera umożliwiło zapobieganiu błędom przy używaniu ułamków.

Babilończycy stosowali tabele ułamków nawet do kilku milionów.

Ułamki były kolejnymi potęgami ujemnymi 60^-1, 60^-2, 60^-3 czyli odpowiednio:

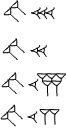
czyli

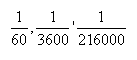
W poniższej tabeli 2 oznacza 1/2, 3 oznacza 1/3, etc.

Ułamek	Zapis ułamka	Zapis 60	Rozwinięcie
2	[0;30]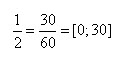
3	[0;20]
4	[0;15]
5	[0;12]
6	[0;10]
8	[0;7;30]
9	[0;6;40]
10	[0;6]
12	[0;5]
15	[0;4]
16	[0;3;45]
18	[0;3;20]
20	[0;3]
24	[0;2;30]
25	[0;2;24]
27	[0;2;13;20]

W powyższej tabeli brak zapisów dla ułamków, które nie są w tym układzie skończone. Takie ułamki zapisywano w przybliżeniu:

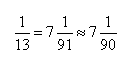
odnotowując, że jest to przybliżenie, a 1/90 odczytywano z tablicy.

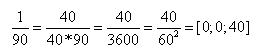
Pierwiastek z 2 obliczano jako:

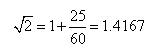
Liczbę Π określano jako 3.

Dzielenie

Babilończycy nie mieli algorytmu dzielenia. Dzielenie opierano na wiedzy, że:

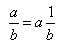
Przy dzieleniu wykorzystywano tablice ułamków.

Aby podzielić 96/16 mnożono 96 przez 1/16:

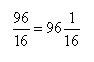czyli mnożono

[1;36] x [0;3,45], co jak widać:

jest trywialnym obliczeniem 🙂

Twierdzenie Pitagorasa

Tabliczka zapisana jest od prawej do lewej

W kolumnie I podane ja jest liczba porządkowa od 1 do 15.

Kolumna II zawiera słowo ‘liczba’.

Kolumna III zaczyna się od słowa ‘długość’, a ponizej zapisane są wartości a.

Kolumna IV zaczyna się od słowa ‘przekątna’, po czym zapisane są kolejne wartości c

Kolumna V zawiera (ponoć) obliczone wartości b

Z obrazka według Historii powszechnej cyfr G. Ifraha str. 418 t. I wynika, że na tabliczce zapisane są dane dotyczące zależności między bokami trójkąta, znane jako twierdzenie Pitagorasa. Niestety nie miałem dostępu do cytowanej literatury, a z prezentowanego przykładu wcale (według mnie) nie wynikają takie zależności. Również podane wielkości nie układają się w trójkąty możliwe do zbudowania. Być może do opisu wkradł się jakiś błąd. Jeśli uda mi się dotrzeć do źródła uzupełnię ten opis. W książce podane są liczby odczytane z tabliczki.

Równania liniowe

Równanie linowe typu:

rozwiązywano korzystając z tablic ułamków.

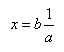
Przy równaniu 6x = 96 obliczano [1;36] x [0;10].

Zadanie z tabliczki klinowej

Bierzemy z z pewnej ilości jęczmienia i dodajemy jeszcze jednostek jęczmienia. Ile mamy jęczmienia?

Rozwiązanie skryby

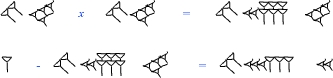
[0;40] x [0;40] = [0;26,40]

[1] – [0;26,40] = [0;33,20]

Odwrotność [0;33,20] odczytujemy z odpowiedniej tablicy: [1;48].

[1;48] x [1; 40] = [3;0]

Rozwiązanie współczesne

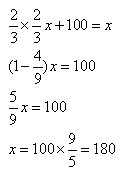
Równania kwadratowe

Babilończycy rozwiązywali równania typu:

Rozwiązanie tego równania wyglądało:

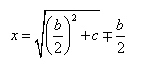
Zwróć uwagę, że jeżeli w równaniu przed b jest ‘-‘ to w rozwiązaniu przed b/2 jest ‘+’ , a
jeżeli w równaniu przed b jest ‘+’ to w rozwiązaniu przed b/2 jest ‘-‘.

Równanie:

rozwiążemy następująco:

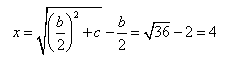
Inne równania

Załóżmy, że mamy równanie:

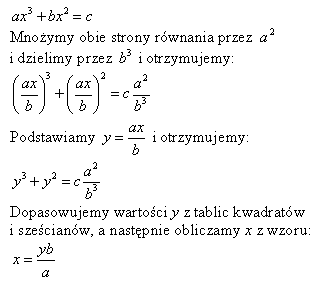
A oto przykład:

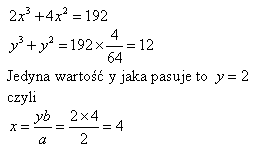
Wola boga Marduka

Miasto Babilon zostało zburzone w czasie najazdu przez króla Sancheriba w 689 r p.n.e. Według przepowiedni z woli boga Marduka miasto miało być odbudowane dopiero po 70 latach od zburzenia. Król Asachardon, który panował w latatach 680 – 669 p.n.e chciał jednak odbudować miasto wcześniej, ale obawiał się ludu, według którego wcześniejsza odbudowa byłaby naruszeniem woli boga Marduka.

Wobec tego wymyślił historię, że początkowo bóg Marduk zapisał na Tabliczce Przeznaczenia liczbę 70 lat, ale potem ogarnięty litością odmienił swoją decyzję i zmienił porządek cyfr. W ten sposób pozwolił aby miasto odbudowano już po 11 latach.

Początkowo liczba na Tabliczce Przeznaczenia wyglądała tak:

Po zmianie wyglądała tak:

Zaiste bóg Marduk był prawdziwie miłosiernym bogiem.

Następna część artykułu