
System sześćdziesiętny (1)
Krótka historia
System ten powstał na terenie Mezopotamii, gdzie posługiwali się nim Sumerowie (już około 4000 r. p.n.e.), następnie Akkadyjczycy (ok. 3000 r. p.n.e), a potem Babilończycy.
Wszystkie te ludy posługiwały się pismem klinowym, a więc i działania matematyczne zapisywano przy użyciu tego pisma.
Pisano na mokrych glinianych tabliczkach, które w razie potrzeby zachowania zapisu – wypalano albo wyrównywano i używano ponownie.
Zarówno język jak i system liczenia czy systemy zapisu to żywe twory, które ulegają ciągłym zmianom. Jeśli chcesz dowiedzieć się więcej na temat dziejów pisma klinowego i systemu sześcdziesiętnego przeczytaj książkę Georga Ifraha Historia powszechna cyfr.
Infrastruktura
Mezopotamczycy budowali miasta z systemami nawadniania. Mieli rozwinięty system prawny, znakomitą administrację. Znali pocztę. Wszystko to wymagało dość zaawansowanej matematyki.
System wiedzy
Babilończycy mieli rozwiniętą astronomię i matematykę. Znano już liczby do setek milionów, pojęcia ułamków, odwrotności, kwadratów i sześcianów liczb. Znano cztery działania oraz potęgowanie i pierwiastkowanie. Umiano obliczać powierzchnie figur i objętości brył geometrycznych. Obliczano pola powierzchni pięciokąta, sześciokąta i siedmiokąta wpisanego w koło. Znano twierdzenie Pitagorasa. Rozwiązywano równania liniowe. Znano algorytm rozwiązywania równań kwadratowych. Rozwiązywano niektóre równania dwukwadratowe i sześcienne. Stosowano tablice matematyczne oraz liczydła (abakusy). Stosowano tabliczki mnożenia, tablice kwadratów, sześcianów, pierwiastków, odwrotności potęg (logarytmów!), tablice pozwalające na obliczenia trójkątów z użyciem twierdzenia Pitagorasa.
To właśnie Babilończycy podzielili dobę na 24 godziny, godzinę na 60 minut, minutę na 60 sekund.
System sześćdziesiętny ma również zastosowanie przy obliczaniu kątów.
System sześćdziesiątkowy babilońskich uczonych
Początkowo system nie był pozycyjny i dopiero Babilończycy zaczęli stosować zapis pozycyjny. Było to prawdopodobnie ich największe osiągnięcie matematyczne.
Prezentujemy tutaj system babilońskich uczonych z ok. XIX stulenia p.n.e, gdy znano już system pozycyjny.
Używane znaki
Używano jedynie 2 znaków:

Liczby od 1 do 59
Z tych cyfr można było ułożyć wszystkie liczby:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cyfra 9 była przedstawiana również jako ![]() albo
albo ![]() .
.
Liczby większe od 59
Liczby zapisywano pozycyjnie:
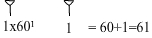
Każda następna liczba po lewej stronie oddzielona spacją od liczby na prawo oznaczała następną potęgę 60:
604 603 602 601 600
A więc liczba ![]() zapisana dziesiętnie:
zapisana dziesiętnie:
2 43 27 11 2 oznaczała:
2×604 + 43×603 + 27×602 + 11×601 + 2×600 czyli
2×12 960 000 + 43×216 000 + 27×3600 + 11×60 + 2×1 czyli
25 920 000 + 9 288 000 + 97 200 + 660 + 2 czyli
35 305 862
Podatność na błędy
Ludzie zawsze popełniali błędy. Pisarz nieuważny, czy pracujący w pośpiechu mógł łatwo pominąć spację. Jak odróżnić:

Pierwsza liczba to 2, druga to 61.
Albo:
Czy to 20 czy 610?
Wynalezienie zera
Jeżeli pisarz wykonywał działanie: ![]() podniesione do kwadratu, to otrzymywał
podniesione do kwadratu, to otrzymywał ![]() , które łatwo mogło być pomylone z
, które łatwo mogło być pomylone z ![]()
(tabl. AO 17264, Luwr).
147 =[2,27]
1472 = 21609 = [6;0;9] czy [6;9] = 369?
Zapewne z powodu tych kłopotów wymyślono zero (ok. 300 r. p.n.e). Zero było przedstawiane jako ![]() .
.
Istniały też inne znaki oznaczające zero.
Tak przedstawiona liczba: ![]() nie budzi żadnych wątpliwości.
nie budzi żadnych wątpliwości.
Tabliczka mnożenia
Babilończycy powszechnie stosowali tablice matematyczne. Np. tabliczka MDP XXXIV tekst IV, tabl. K, Luwr ułatwia mnożenie danej liczby przez 25:
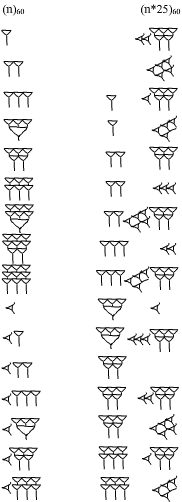
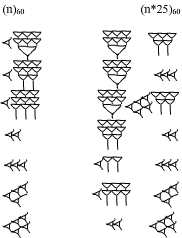
W transkrypcji wygląda to tak:
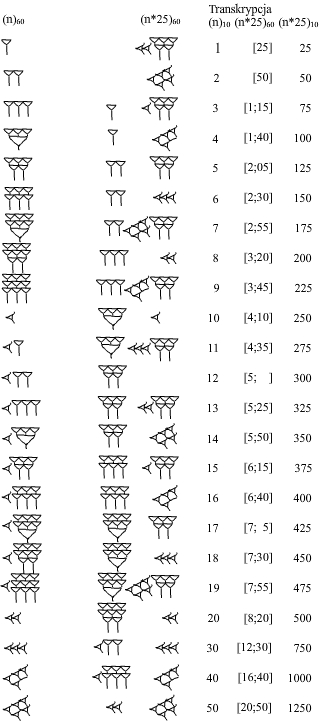
W oryginale tabliczki jest błąd przy liczbie 19. Podane liczby w transkrypcji były [7;45], czyli [465], co nie jest prawdą!
Mnożenie przez 25 z użyciem tabliczki mnożenia
Mnożymy 692 = [11;32] x 25
Po prawej stronie umieszczamy mnożną.
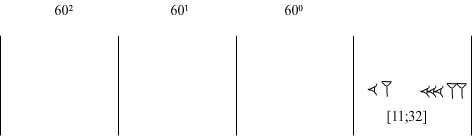
W tabliczce mnożenia przez 25 szukamy iloczynu odpowiadającego liczbie 2. Jest to liczba 50. Umieszczamy ją w kolumnie jedności:
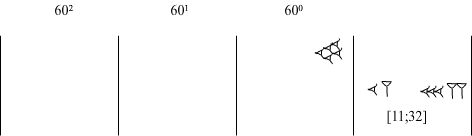
Z zapisu 32 po prawej stronie usuwamy 2, gdyż zostało już wykorzystane. W tabliczce mnożenia przez 25 szukamy odpowiednika liczby 30. Jest to liczba [12;30]. 30 umieszczamy w kolumnie jedności, a 12 w kolumnie 601
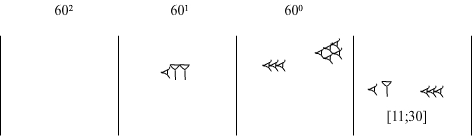
Ponieważ 30 już wykorzystaliśmy usuwamy go z obliczeń. W tabliczce mnożenia przez 25 szukamy odpowiednika dla liczby 11. Jest to liczba [4;35]. 35 zapisujemy w kolumnie 601, a liczbę 4 w kolumnie 602.
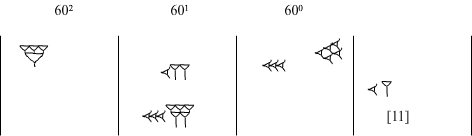
Usuwamy 11 ponieważ zostało już wykorzystane. Porządkujemy wyniki. W kolumnie 600 jest 8 'gwoździ’. 6 z nich usuwamy, a w kolumnie 601 dodajemy 1. W ten sposób w kolumnie 600 pozostają dwa 'gwoździe’
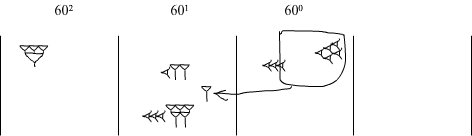
W kolumnie 601 mamy teraz 4 'haki’ i 8 'gwoździ’ Usuwamy je wszystkie i zastępujemy liczbą 48.
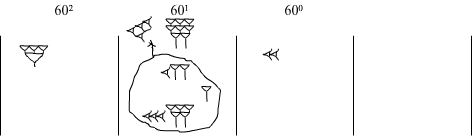
Układamy ładnie i odczytujemy wynik:
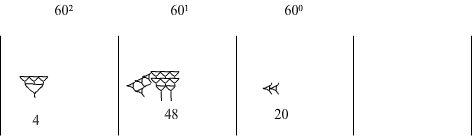
Wynik to [4;48;20] = 4×602 + 48×60 + 20 = 14 400 + 2 880 + 20 = 17 300

