
Liczby Stirlinga I rodzaju (dla cykli)
Opisują rozmieszczenie n liczb w k cyklach.
Oznaczane są symbolem 
Wiadomo, że
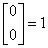
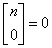
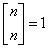
Dla k > n:
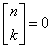
Kolejne liczby obliczamy z rekurencyjnego wzoru:
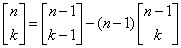
Część liczb będzie ujemna. Jeżeli chcesz pozbyć się minusów należy użyć wzoru:
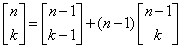
Możemy to ująć w tabelce:
| n\k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||||
| 1 | 0 | 1 | |||||||
| 2 | 0 | -1 | 1 | ||||||
| 3 | 0 | 2 | -3 | 1 | |||||
| 4 | 0 | -6 | 11 | -6 | 1 | ||||
| 5 | 0 | 24 | -50 | 35 | -10 | 1 | |||
| 6 | 0 | -120 | 274 | -225 | 85 | -15 | 1 | ||
| 7 | 0 | 720 | -1764 | 1624 | -735 | 175 | -21 | 1 | |
| 8 | 0 | -5040 | 13068 | -13132 | 6769 | -1960 | 322 | -28 | 1 |
Gdy chcesz obliczyć liczbę permutacji n elementów o dokładnie k cyklach użyj wzoru:
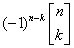
Przykład
Liczba permutacji zbioru 4 elementowego złożonego z 2 cykli wynosi 11 .
Możemy je wszystkie wypisać, aby to sprawdzić:
(0,1,2)(3)
(0,2,1)(3)
(0,1,3)(2)
(0,3,1)(2)
(0,2,3)(1)
(0,3,2)(1)
(1,2,3)(0)
(1,3,2)(0)
(0,1)(2,3)
(0,2)(1,3)
(0,3)(1,2)
Sprawdzamy:
Start 11 Koniec
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

