Liczby Stirlinga II rodzaju (dla podzbiorów)

Liczby Stirlinga II rodzaju (dla podzbiorów)

Opisują liczbę sposobów podziału zbioru n elementowego na k niepustych podzbiorów.

Symbol Stirlinga 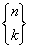. Czytamy “k podzbiorów n”.

Wiemy, że:

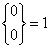
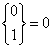
Dla n > 0:

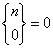
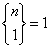
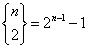
Dla n < k:

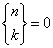
Dla n = k:

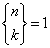
Kolejne liczby obliczamy z rekurencyjnego wzoru:

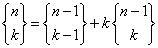dla n > 0

Aby ułatwić zapis sprowadzimy liczby do parteru:

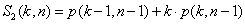
Wykonajmy parę obliczeń:

 

 

 

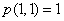
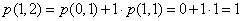
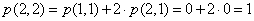
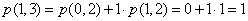
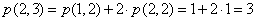
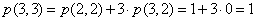
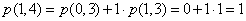
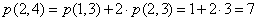
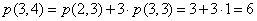
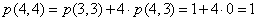
Możemy to ująć w tabelce:

Liczby Stirlinga II rodzaju

n\k	0	1	2	3	4	5	6	7	8	9	10
0	1
1	0	1
2	0	1	1
3	0	1	3	1
4	0	1	7	6	1
5	0	1	15	25	10	1
6	0	1	31	90	65	15	1
7	0	1	63	301	350	140	21	1
8	0	1	127	966	1701	1050	266	28	1
9	0	1	255	3025	7770	6951	2646	462	36	1
10	0	1	511	9330	34105	42525	22827	5880	750	45	1

Równoważnym wzorem jest:

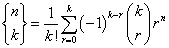
Przykład

Liczba podziałów zbioru 4 elementowego złożonego na 2 elementowe podzbiory wynosi 7 .

Możemy je wszystkie wypisać, aby to sprawdzić:

{0,1,2}{3}
{0,1,3}{2}
{0,2,3}{1}
{1,2,3}{0}
{0,1}{2,3}
{0,2}{1,3}
{0,3}{1,2}

Sprawdzamy:

Start
7
Koniec

Kody

Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.

Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

Copyright Jacek Piechota, Opublikowano 30 marca 2016