
Liczby Bella
Liczby Bella pozwalają obliczyć ile niepustych podzbiorów dowolnej wielkości można utworzyć z n rozróżnialnych elementów.
Używamy wzoru:
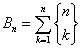
albo
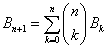
Zadanie
Ile niepustych podzbiorów dowolnej wielkości można utworzyć z 3 rozróżnialnych elementów.
Rozwiązanie:
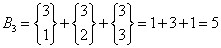
Sprawdzamy
Elementy: 1,2,3
Podzbiory:
{{1,2,3}}
{{1,2}{3}}
{{1,3}{2}}
{{2,3}{1}}
{{1}{2}{3}}
Sprawdzamy
n = 3 bell(3) = 5
A oto 70 pierwszych liczb Bella:
1: 1 2: 2 3: 5 4: 15 5: 52 6: 203 7: 877 8: 4140 9: 21147 10: 115975 11: 678570 12: 4213597 13: 27644437 14: 190899322 15: 1382958545 16: 10480142147 17: 82864869804 18: 682076806159 19: 5832742205057 20: 51724158235372 21: 474869816156751 22: 4506715738447323 23: 44152005855084346 24: 445958869294805289 25: 4638590332229999353 26: 49631246523618756274 27: 545717047936059989389 28: 6160539404599934652455 29: 71339801938860275191172 30: 846749014511809332450147 31: 10293358946226376485095653 32: 128064670049908713818925644 33: 1629595892846007606764728147 34: 21195039388640360462388656799 35: 281600203019560266563340426570 36: 3819714729894818339975525681317 37: 52868366208550447901945575624941 38: 746289892095625330523099540639146 39: 10738823330774692832768857986425209 40: 157450588391204931289324344702531067 41: 2351152507740617628200694077243788988 42: 35742549198872617291353508656626642567 43: 552950118797165484321714693280737767385 44: 8701963427387055089023600531855797148876 45: 139258505266263669602347053993654079693415 46: 2265418219334494002928484444705392276158355 47: 37450059502461511196505342096431510120174682 48: 628919796303118415420210454071849537746015761 49: 10726137154573358400342215518590002633917247281 50: 185724268771078270438257767181908917499221852770 51: 3263983870004111524856951830191582524419255819477 52: 58205338024195872785464627063218599149503972126463 53: 1052928518014714166107781298021583534928402714242132 54: 19317287589145618265728950069285503257349832850302011 55: 359334085968622831041960188598043661065388726959079837 56: 6775685320645824322581483068371419745979053216268760300 57: 129482661947506964462616580633806000917491602609372517195 58: 2507136358984296114560786627437574942253015623445622326263 59: 49176743336309621659000944152624896853591018248919168867818 60: 976939307467007552986994066961675455550246347757474482558637 61: 19652364471547941482114228389322789963345673460673370562378245 62: 400237304821454786230522819234667544935526963060240082269259738 63: 8250771700405624889912456724304738028450190134337110943817172961 64: 172134143357358850934369963665272571125557575184049758045339873395 65: 3633778785457899322415257682767737441410036994560435982365219287372 66: 77605907238843669482155930857960017792778059887519278038000759795263 67: 1676501284301523453367212880854005182365748317589888660477021013719409 68: 36628224206696135478834640618028539032699174847931909480671725803995436 69: 809212768387947836336846277707066239391942323998649273771736744420003007 70: 18075003898340511237556784424498369141305841234468097908227993035088029195
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

