Naszyjniki i bransoletki

Liczby względnie pierwsze

Jak wiemy z rozdziału poświęconego liczbom pierwszym każda liczba większa od 1 jest iloczynem liczb pierwszych lub sama jest liczbą pierwszą (czyli iloczynem siebie i 1):

7 jest liczbą pierwszą
14 = 2 * 7
15 = 3 * 5
21 = 3 * 7

Liczby względnie pierwsze to takie liczby całkowite, które po rozłożeniu na czynniki pierwsze nie mają wspólnych czynników (dzielników) poza 1.

4 i 15 są liczbami względnie pierwszymi
14 i 21 nie są względnie pierwsze gdyż obie dzielą się przez 7
15 i 21 nie są względnie pierwsze gdyż obie dzielą się przez 3

Aby sprawdzić, czy liczby są względnie pierwsze, najlepiej użyć funkcji obliczającej największy wspólny dzielnik (NWD). Jeżeli NWD = 1 to liczby są względnie pierwsze

Funkcja φ Eulera

Nazywana jest również funkcją φ Gaussa lub tocjentem.

Funkcja φ(n) oblicza liczbę liczb względnie pierwszych z n, które są większe lub równe 1 i mniejsze od n, czyli spełniają warunek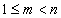

n	1	2	3	4	5	6	7	8	9	10	11	12
φ(n)	1	1	2	2	4	2	6	4	6	4	10	4
liczby względnie pierwsze z n	1	1	1,2	1,3	1,2,3,4	1,5	1,2,3,4,5,6	1,3,5,7	1,2,4,5,7,8	1,3,7,9	1,2,3,4,5,6,7,8,9,10	1,5,7,11
czynniki pierwsze n	–	2	3	2×2=22	5	2×3	7	2x2x2=23	3×3=32	2×5	11	2x2x3=22x3

Wzór:

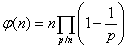
gdzie:

Π oznacza ‘iloczyn’

p oznacza dzielnik pierwszy liczby n.

p|n oznacza, że składnikami iloczynu są wszystkie dzielniki pierwsze liczby n (bez powtórzeń, czyli składnik jest uwzględniany tylko raz)

Przykład 1

Liczba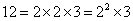

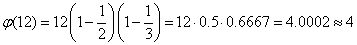
Istnieją 4 liczby względnie pierwsze z n (1,5,7,11);

Przykład 2

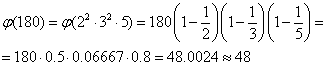
Właściwości

Właściwość 1

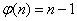gdy n jest liczbą pierwszą.

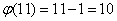
Właściwość 2

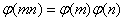, jeżeli m i n są względnie pierwsze.

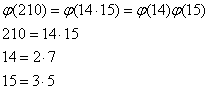
Liczby 14 i 15 są względnie pierwsze.

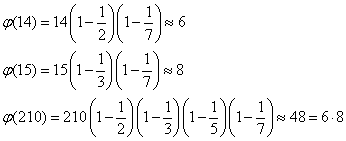
Właściwość 3

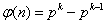jeżeli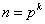

Ponieważ 8 = 2³ to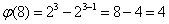

Właściwość 4

Dla dowolnej liczby całkowitej n zachodzi:

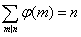
Sumowanie przebiega po wszystkich dzielnikach m liczby n.

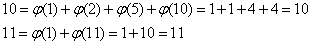
Właściwość 5

Jeżeli

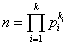
jest rozkładem liczby n na czynniki pierwsze to:

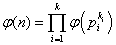
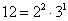
więc

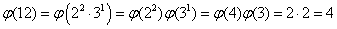
Tabela wartości funkcji tocjent i wykaz liczb względnie pierwszych

Naszyjniki i bransoletki

Naszyjnik składa się z n koralików, z których każdy może być w jednym z k kolorów.

Naszyjnik jest też (rozpiętym) łańcuchem zawierającym n znaków wziętych z alfabetu mającego k znaków.

Wszelkie naszyjniki powstałe przez obrót (rotację) są uważane za równoważne.

Naszyjnik kombinatoryczny podobnie jak jubilerski ma tylko jedną stronę, czyli jeden układ ‘koralików’.

Bransoletka kombinatoryczna podobnie jak jubilerska, jest podobna do naszyjnika, ale ma dwie strony. Drugą stronę uzyskujemy dokonując refleksji (odbicia).

Poniżej przedstawiamy naszyjniki i bransoletki dla n = 6 i k = 2.

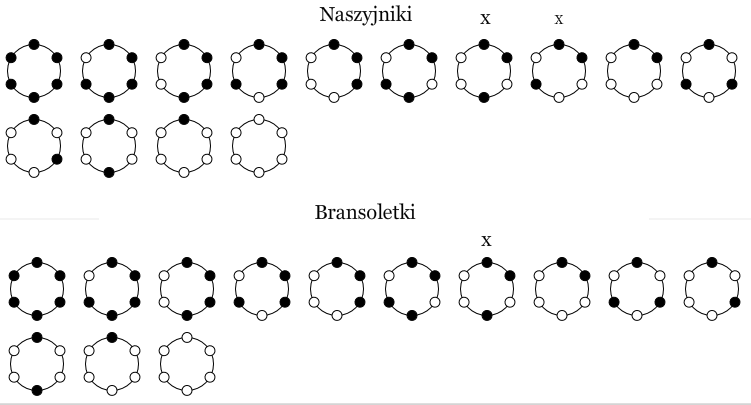
Liczba naszyjników N₂(6) = 14

Liczba bransoletek B₂(6) = 13

Układ oznaczony jako x to dwa układy w sensie naszyjników, a jeden układ w sensie bransoletek.

Układ ten wykazuje symetrię chiralną, która występuje wtedy, gdy dwie figury nie dadzą się na siebie nałożyć jedynie przez translację (przesunięcie) i rotację (obrót), ale można je nałożyć przez refleksję (odbicie).

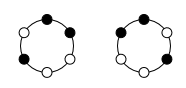
Po odwróceniu jednego z zaznaczonych układów otrzymujemy drugi, więc ponieważ naszyjników nie można odwracać, liczymy je jako dwa układy. Ponieważ bransoletki możemy odwracać liczmy je jako jedną bransoletkę.

Naszyjniki

Liczbę naszyjników można obliczyć ze wzoru:

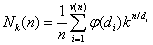
gdzie:

n – to liczba elementów

k – to liczba stanów (kolorów), które może przyjąć każdy z koralików

d_i są dzielnikami n od d₁ = 1 do d_v = n. v(n) jest liczbą dzielników n.

φ(d_i) – oznacza funkcję φ Eulera, nazywaną czasem funkcją Gaussa.

Przykład 1

Obliczmy N dla n = 10 i k = 2

Dzielniki liczby 10 to {1, 2, 5, 10}

φ(1) = 1

φ(2) = 1

φ(5) = 4

φ(10) = 4

Tablice naszyjników

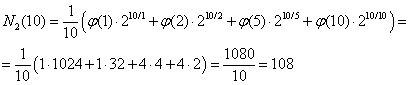
Bransoletki

Liczbę bransoletek możemy obliczyć ze wzoru:

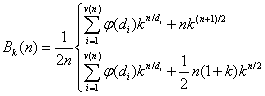
Wzoru umieszczonego wyżej używamy gdy n jest liczbą nieparzystą.

Wzoru umieszczonego niżej używamy, gdy n – jest liczbą parzystą.

N_k(n) – oznacza liczbę naszyjników

Powyższy wzór można uprościć:

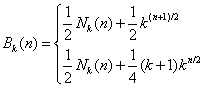
Wzoru umieszczonego wyżej używamy gdy n jest liczbą nieparzystą.

Wzoru umieszczonego niżej używamy, gdy n – jest liczbą parzystą.

Gdy k = 2, a n jest nieparzystą liczbą pierwszą (czyli większą od 2), wzór upraszcza się do:

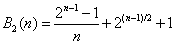
Przykład 2

Obliczamy liczbę bransoletek dla n = 10 i k = 2

Skorzystamy ze wzoru uproszczonego.

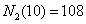
Ponieważ n jest liczbą parzystą:

Tablice bransoletek

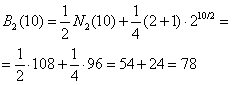
Kody

Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.

Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

Copyright Jacek Piechota, Opublikowano 9 kwietnia 2016