
Liczby Catalana
Nazywane również liczbami Segnera.
Wzór:
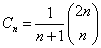
Wiemy, że:
C0 = 0
C1 = 1
A oto pierwsze 100 liczb Catalana:
1: 1 2: 2 3: 5 4: 14 5: 42 6: 132 7: 429 8: 1430 9: 4862 10: 16796 11: 58786 12: 208012 13: 742900 14: 2674440 15: 9694845 16: 35357670 17: 129644790 18: 477638700 19: 1767263190 20: 6564120420 21: 24466267020 22: 91482563640 23: 343059613650 24: 1289904147324 25: 4861946401452 26: 18367353072152 27: 69533550916004 28: 263747951750360 29: 1002242216651368 30: 3814986502092304 31: 14544636039226909 32: 55534064877048198 33: 212336130412243110 34: 812944042149730764 35: 3116285494907301262 36: 11959798385860453492 37: 45950804324621742364 38: 176733862787006701400 39: 680425371729975800390 40: 2622127042276492108820 41: 10113918591637898134020 42: 39044429911904443959240 43: 150853479205085351660700 44: 583300119592996693088040 45: 2257117854077248073253720 46: 8740328711533173390046320 47: 33868773757191046886429490 48: 131327898242169365477991900 49: 509552245179617138054608572 50: 1978261657756160653623774456 51: 7684785670514316385230816156 52: 29869166945772625950142417512 53: 116157871455782434250553845880 54: 451959718027953471447609509424 55: 1759414616608818870992479875972 56: 6852456927844873497549658464312 57: 26700952856774851904245220912664 58: 104088460289122304033498318812080 59: 405944995127576985730643443367112 60: 1583850964596120042686772779038896 61: 6182127958584855650487080847216336 62: 24139737743045626825711458546273312 63: 94295850558771979787935384946380125 64: 368479169875816659479009042713546950 65: 1440418573150919668872489894243865350 66: 5632681584560312734993915705849145100 67: 22033725021956517463358552614056949950 68: 86218923998960285726185640663701108500 69: 337485502510215975556783793455058624700 70: 1321422108420282270489942177190229544600 71: 5175569924646105559418940193995065716350 72: 20276890389709399862928998568254641025700 73: 79463489365077377841208237632349268884500 74: 311496878311103321137536291518809134027240 75: 1221395654430378811828760722007962130791020 76: 4790408930363303911328386208394864461024520 77: 18793142726809884575211361279087545193250040 78: 73745243611532458459690151854647329239335600 79: 289450081175264899454283846029490767264392230 80: 1136359577947336271931632877004667456667613940 81: 4462290049988320482463241297506133183499654740 82: 17526585015616776834735140517915655636396234280 83: 68854441132780194707888052034668647142985206100 84: 270557451039395118028642463289168566420671280440 85: 1063353702922273835973036658043476458723103404520 86: 4180080073556524734514695828170907458428751314320 87: 16435314834665426797069144960762886143367590394940 88: 64633260585762914370496637486146181462681535261000 89: 254224158304000796523953440778841647086547372026600 90: 1000134600800354781929399250536541864362461089950800 91: 3935312233584004685417853572763349509774031680023800 92: 15487357822491889407128326963778343232013931127835600 93: 60960876535340415751462563580829648891969728907438000 94: 239993345518077005168915776623476723006280827488229600 95: 944973797977428207852605870454939596837230758234904050 96: 3721443204405954385563870541379246659709506697378694300 97: 14657929356129575437016877846657032761712954950899755100 98: 57743358069601357782187700608042856334020731624756611000 99: 227508830794229349661819540395688853956041682601541047340 100: 896519947090131496687170070074100632420837521538745909320
Liczbę dla dużych n można obliczyć z wzoru:
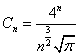
Liczby Catalana spełniają zależność:
Dla 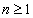
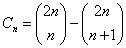
Zastosowania
Liczba dróg
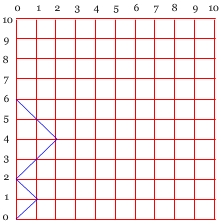
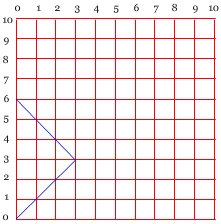
Możemy wyrazić n-tą liczbą Catalana ilość wszystkich łamanych „dróg” zaczynających się w początku układu współrzędnych, a kończących się w punkcie (0,2n). Każda z nich złożona jest z pojedynczych odcinków położonych w I ćwiartce układu o początku (x,y) i końcu (x+1,y+1), albo (x-1,y+1), gdzie x i y są liczbami naturalnymi.
Ogranicznikiem od góry jest 2n, a z prawej n.
Przykład
Zbadać liczbę dróg od punktu (0,0) do punktu (0,6).
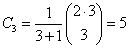
Sprawdzamy
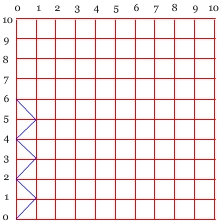
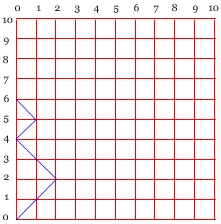
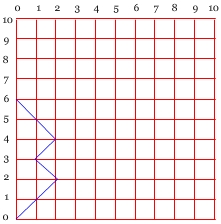
Liczba rozmieszczeń nawiasów
Znak '*’ może być zastąpiony przez '+’, ’-’, 'x’ lub '/’.
Ile wyników można otrzymać dla wyrażenia mającego n zmiennych
Dla danego n liczba Cn-1 wyraża liczbę możliwych wyników.
Przykład 1
n = 3
C2= 2 (z tabeli)
Sprawdzamy:
(a * b) * c
a * (b * c)
Przykład 2
n = 4
C3= 5 (z tabeli)
Sprawdzamy:
(a * b) * (c * d)
a * (b * c) * d
a * (b * (c * d))
((a * b) * c) * d
a* ((b * c) * d)
Liczba podziałów na trójkąty
Liczbę sposobów podziału wielokąta wypukłego, która ma n+2 krawędzi na różne trójkąty za pomocą przekątnych wynosi Cn.
Przykład 2
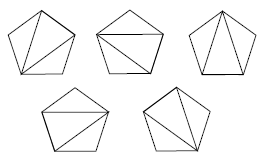
Ile jest sposobów podziału piiokąta foremnego na różne trójkąty za pomocą przekątnych.
C5-2 = C3 = 5 (z tablicy)
Przykład 2
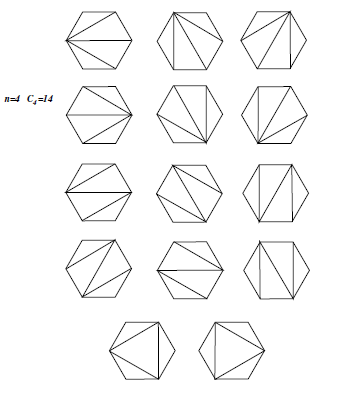
Ile jest sposobów podziału sześciokąta foremnego na różne trójkąty za pomocą przekątnych.
C6-2 = C4 = 14 (z tablicy)
Liczba monotonicznych dróg
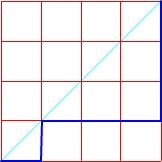
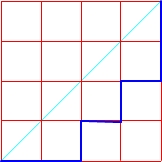
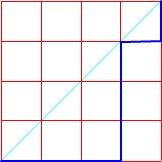
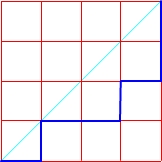
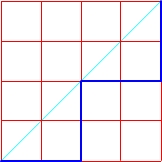
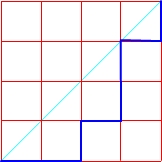
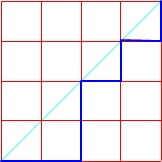
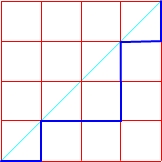
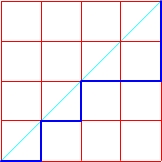
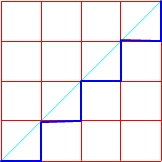
Mając kwadrat o boku n, możemy za pomocą n-tej liczby Catalana policzyć ilość wszystkich możliwych monotonicznych dróg rozpoczynających się z dolnego lewego wierzchołka, prowadzących do górnego prawego, takich, żeby nigdy nie przekraczać przekątnej, która łączy te wierzchołki.
Przykład
Drogi w kwadracie o boku n = 4
C4 = 14
Sprawdzamy:
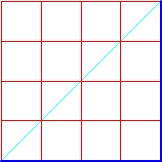
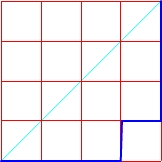
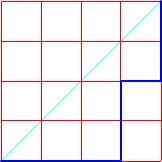
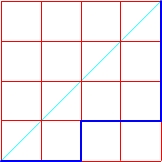
Liczba drzew binarnych
Cn jest równe liczbie różnych ukorzenionych regularnych drzew binarnych o n+ 1 liściach.
oraz
Cn jest równe liczbie różnych ukorzenionych regularnych drzew binarnych o n wierzchołkach wewnętrznych.
Ukorzenione płaskie drzewo binarne składa się z wyróżnionego wierzchołka (korzenia) oraz pary ukorzenionych płaskich drzew binarnych (lewego i prawego pod-drzewa). Z każdego wierzchołka, za wyjątkiem korzenia z którego wychodzi tylko pień, wychodzą albo dwie gałęzie (lewa i prawa gałąź) albo nie wychodzą gałęzie. W pierwszym przypadku wierzchołek jest nazywany wewnętrznym, w drugim przypadku jest nazywany zewnętrznym lub liściem.
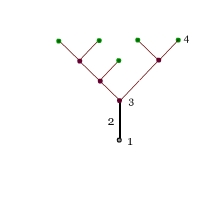
1 – korzeń
2 – pień
3 – rozgałęzienie (wierzchołek wewnętrzny)
4 – liść (wierzchołek zewnętrzny)
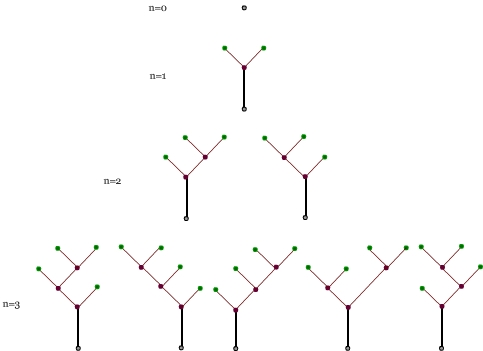
Drzewa dla różnych liczb wierzchołków wewnętrznych.
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

