
Liczba fi (φ) i złoty podział
Liczba fi (φ)
Nazywana również liczbą złotego podziału albo złotą liczbą.
Jest rozwiązaniem zadania:
„Podziel odcinek na dwie części tak, aby część większa miała się tak do mniejszej jak całość do większej”.
Rozwiązaniem jest liczba:
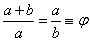
Po obliczeniu:
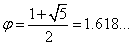
A oto pierwsze 1000 liczb rozwinięcia:
1.61803398874989484820458683436563811772030917980576 28621354486227052604628189024497072072041893911374 84754088075386891752126633862223536931793180060766 72635443338908659593958290563832266131992829026788 06752087668925017116962070322210432162695486262963 13614438149758701220340805887954454749246185695364 86444924104432077134494704956584678850987433944221 25448770664780915884607499887124007652170575179788 34166256249407589069704000281210427621771117778053 15317141011704666599146697987317613560067087480710 13179523689427521948435305678300228785699782977834 78458782289110976250030269615617002504643382437764 86102838312683303724292675263116533924731671112115 88186385133162038400522216579128667529465490681131 71599343235973494985090409476213222981017261070596 11645629909816290555208524790352406020172799747175 34277759277862561943208275051312181562855122248093 94712341451702237358057727861600868838295230459264 78780178899219902707769038953219681986151437803149 97411069260886742962267575605231727775203536139362
Liczba ta ma kilka interesujących właściwości:
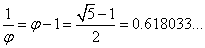
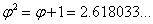
Liczba φ w geometrii
Złoty podział odcinka

a = 116.8
b = 100
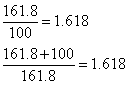
Złoty podział nazywany jest też złotym stosunkiem, boską proporcją, boskim podziałem, złotą proporcją, złotym cięciem.
Złoty prostokąt
Złoty prostokąt to prostokąt o stosunku dłuższego boku (a + b) do krótszego boku a równym φ

Każdy taki prostokąt można podzielić na kwadrat o boku a oraz złoty prostokąt o dłuższym boku a i krótszym boku b.
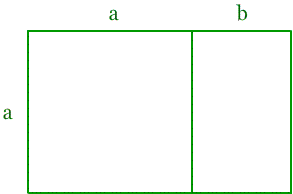
Taki podział można kontynuować w nieskończoność.
Złota spirala
Jeśli powtórzymy wielokrotnie operację odcinania prostokątów, a w każdy kwadrat po odcięciu prostokąta wpiszemy ćwiartkę okręgu – otrzymamy tzw. złotą spiralę.
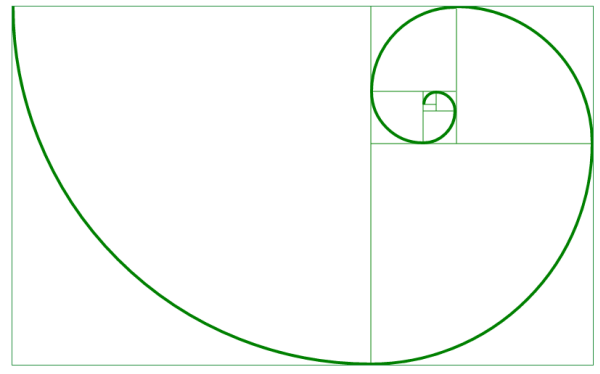
Złoty trójkąt
Złoty trójkąt to trójkąt równoramienny, w którym stosunek boku (a + b) do podstawy a jest równy liczbie φ:
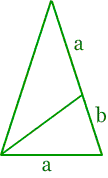
Złoty trójkąt można podzielić na dwa trójkąty, z których jeden ma proporcje boku do podstawy (po dokonaniu obrotu) 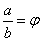
Ten podział można kontynuować w nieskończoność.
Ze złotego trójkąta również można otrzymać złotą spiralę.
Pentagram

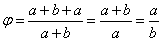
Liczba φ w architekturze
W wielu opracowaniach pojawiają się informacje dotyczące Partenonu, czy piramid w Gizie
Bryła Partenonu jest zbliżona do złotego prostokąta.
Co do piramid istnieje wiele sprzecznych doniesień. Większość uczonych skłania się do poglądu, że występowanie proporcji związanych z liczbą φ jest dziełem przypadku, gdyż starożytni Egipcjanie nie znali ani liczby φ ani π. Co najwyżej dopatrują się proporcji 3 : 4 : 5
Liczba φ w malarstwie i rzeźbie
Apollo Belwederski
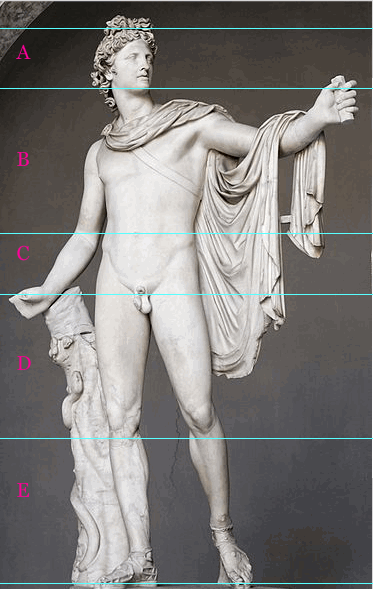
Odległości względne (z miarki w programie ilustracyjnym) wynoszą:
A = 50, B = 145, C = 60, D = 145, E = 135
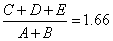
Jak widzimy proporcja zgadza się jedynie w przybliżeniu.
Warto też prześledzić inne zależności z obrazka.
Z pewnością wielu artystów stosowało złoty podział w swoich dziełach. Szczególnie często omawiany jest przykład Sakrament Ostatniej WieczerzySalvadora Dali.
W wielu dziełach proporcje są inne, ewentualnie zbliżone do liczby φ
Liczba φ w muzyce
W opracowaniach dotyczących tematu często cytuje się poniższą tabelkę, ale niestety nie potrafię się do jej prawidłowości ustosunkować.
| Współczynnik Fibonacciego | Przybliżona częstotliwość | Nuta |
|---|---|---|
| 1/1 | 440,00 | A |
| 2/1 | 880,00 | A |
| 2/3 | 293,66 | D |
| 2/5 | 174,62 | F |
| 3/2 | 659,26 | E |
| 3/5 | 261,61 | C |
| 3/8 | 164,82 | E |
| 5/2 | 1108,72 | Cis |
| 5/3 | 740,00 | Fis |
| 5/8 | 277,18 | Cis |
| 8/3 | 1174,64 | D |
| 8/5 | 698,46 | F |
Wśród utworów zawierających odniesienia do złotego podziału wymienia się utwory:
- Béli Bartók: Muzyka na smyczki, perkusję i czelestę
- Erik Satie; Sonneries de la Rose+Croix
- Debussy: Reflets dans l’eau
Muzykolodzy twierdzą, że dzieła oparte na złotym podziale i ciągu Fibonacciego są na ogół kiepskimi dziełami muzycznymi. Wszystkie takie próby uznaje się za nieudane.
Liczba φ w proporcjach ludzkiego ciała
Dłoń
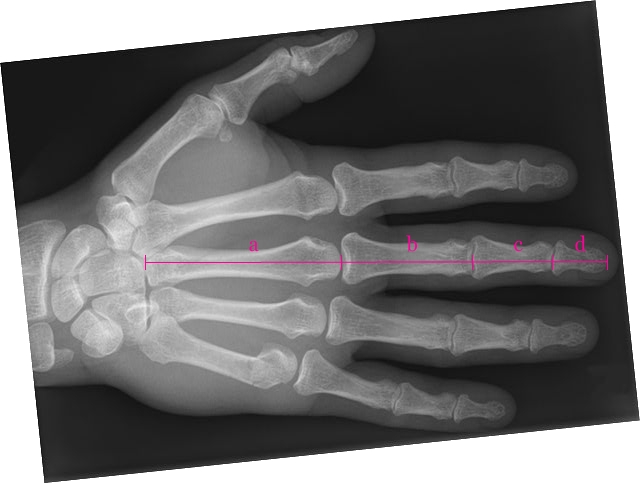
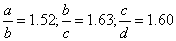
Jak widzimy proporcje zgadzają się w przybliżeniu.
Podobnych proporcji badacze dopatrują się również w proporcjach ludzkiej ręki.
Liczba φ w przyrodzie
Większość doniesień dotyczących obecności złotych proporcji czy złotych podziałów w organizmach żywych, nie odpowiada prawdzie.
Dokładne pomiary nie potwierdzają istnienia takich proporcji, a co najwyżej proporcji zbliżonych. Oczywiście – odchylenia mogą być warunkowane działaniem przypadku, gdyż (niemal) każdy organizm jest inny.
Zloty podział jest podstawą cyklu fal mózgowych.
Złoty podział jest obecny w skali atomowej w rezonansie magnetycznym spinów w kryształach niobanu kabaltu.
Istnieją sugestie, że złotego podziału można dopatrzeć się w ludzkim genomie, szczególnie w strukturze przestrzennej DNA.
Liczba φ w technice
Złoty podział jest powszechnie stosowany i widoczny np. w kształtach pocztówek, kart do gry, plakatów, szerokoekranowych telewizorów, zdjęć, włączników światła, etc.
Liczba φ w ekonomii
Próbuje się stosować złoty podział i liczby Fibonacciego w analizach ekonomicznych, np. analizie trendów wzrostu i spadku wartości akcji na giełdzie. Dokładniejsze obserwacje pokazują, że istnieją jedynie co najwyżej przybliżone i krótkotrwałe podobieństwa.
Część jest omówiona w artykule o liczbach i ciągu Fibonacciego.
Wątpliwości
Informacje, że obiekty o złotych proporcjach, są uważane za bardziej estetyczne, nie są potwierdzone przez badania naukowe.

