
Najmniejsza wspólna wielokrotność (nwd)
Najmniejsza wspólna wielokrotność liczb a i b to najmniejsza liczba, która dzieli się bez reszty zarówno przez a jak i b.
Najmniejszą wspólną wielokrotnością liczb 3 i 5 jest 15.
Najmniejszą wspólną wielokrotność oznaczamy jako nww albo nww(a, b).
nww(3, 5)=15.
Obliczanie przez rozkład na czynniki pierwsze
Największa wspólna wielokrotność jest iloczynem wszystkich czynników pierwszych występujących w rozkładzie obu liczb, z tym że, dany czynnik pierwszy występuje w tym iloczynie tyle razy, ile razy występował w rozkładzie, w którym pojawił się największą liczbę razy.
Przykład
Liczba a = 56 = 2⋅2⋅2⋅7
Liczba b = 42 = 2⋅3⋅7
nww(56, 14) = 2⋅2⋅2⋅3⋅7 = 168
Obliczanie z największego wspólnego dzielnika (nwd)
Ponieważ
![]()
więc
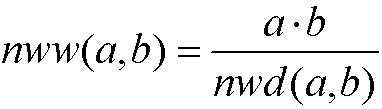
Prawdziwa jest też zależność
![]()
Obliczanie dla trzech liczb
nww możemy obliczyć dla trzech liczb biorąc pod uwagę, że
![]()
Przykład
![]()
Przez analogię możemy obliczyć największą wspólną wielokrotność dla dowolnej liczby liczb.
Zastosowania
Najmniejsza wspólna wielokrotność (nww) jest wykorzystywana do:
- Redukcji ułamków do postaci nieskracalnej

