
Liczby Eulera II rodzaju (rzędu)
Gdy mamy do czynienia z permutacjami multizbioru {1,1,2,2,…,n,n} to liczba Eulera II rodzaju (rzędu) 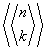 określa liczbę permutacji mających dokładnie k wzniesień. Dodatkowo warunkiem jest aby wszystkie liczby występujące między każdą parą liczb m były większe od m. Gdy dwie liczby m występują bezpośrednio po sobie warunek uznaje się za spełniony.
określa liczbę permutacji mających dokładnie k wzniesień. Dodatkowo warunkiem jest aby wszystkie liczby występujące między każdą parą liczb m były większe od m. Gdy dwie liczby m występują bezpośrednio po sobie warunek uznaje się za spełniony.
Dokładnie ta sama liczba permutacji wystąpi, gdy wszystkie liczby występujące między parą liczb m są mniejsze od m, tyle, że wtedy otrzymujemy – oczywiście – całkiem inny zestaw liczb.
Liczba permutacji multizbioru to 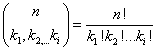 , a liczba permutacji spełniających warunek obliczana jest z wzoru na silnie:
, a liczba permutacji spełniających warunek obliczana jest z wzoru na silnie: 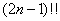
Liczby Eulera obliczamy z wzoru rekurencyjnego:
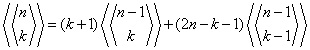
Wiemy, że: 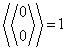 ,
, 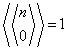 ,
, 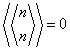
Przykład
Mamy multizbiór: {1,1,2,2,3,3}
Liczba permutacji jest równa 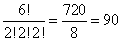
112233, 112323, 112332, 113223, 113232, 113322, 121233, 121323, 121332,
122133, 122313, 122331, 123123, 123132, 123213, 123231, 123312, 123321,
131223, 131232, 131322, 132123, 132132, 132213, 132231, 132312, 132321,
133122, 133212, 133221, 211233, 211323, 211332, 212133, 212313, 212331,
213123, 213132, 213213, 213231, 213312, 213321, 221133, 221313, 221331,
223113, 223131, 223311, 231123, 231132, 231213, 231231, 231312, 231321,
232113, 232131, 232311, 233112, 233121, 233211, 311223, 311232, 311322,
312123, 312132, 312213, 312231, 312312, 312321, 313122, 313212, 313221,
321123, 321132, 321213, 321231, 321312, 321321, 322113, 322131, 322311,
323112, 323121, 323211, 331122, 331212, 331221, 332112, 332121, 332211
Liczba permutacji z wzniesieniami spełniających podany warunek równa się:
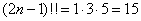
| n | k | 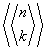 |
partycje |
|---|---|---|---|
| 3 | 0 | 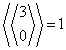 |
332211 |
| 1 | 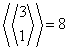 |
113322 133221 221133 221331 223311 233211 331122 331221 |
|
| 2 | 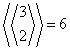 |
112233 112332 122133 122331 123321 133122 |
|
| Suma | 15 | ||
Kryteria wyboru:
- 312312 – między jedynkami jest 2 i 3 (OK), ale między dwójkami 3 i 1 – nie spełnia warunku, między trójkami jest 1 i 2 – nie spełnia warunku
- 123321 – między jedynkami jest 2 i 3 (OK), między dwójkami jest 3 (OK) spełnia warunki – ma dwa wzniesienia: liczbę 2 i liczbę 3
| k | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n, | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 1 | 2 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 1 | 8 | 6 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 1 | 22 | 58 | 24 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 1 | 52 | 328 | 444 | 120 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 1 | 114 | 1452 | 4400 | 3708 | 720 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 1 | 240 | 5610 | 32120 | 58140 | 33984 | 5040 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 1 | 494 | 19950 | 195800 | 644020 | 785304 | 341136 | 40320 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 1 | 1004 | 67260 | 1062500 | 5765500 | 12440064 | 11026296 | 3733920 | 362880 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 1 | 2026 | 218848 | 5326160 | 44765000 | 155357384 | 238904904 | 162186912 | 44339040 | 3628800 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

