
Mnożenie macierzy (Java)
Mnożenie macierzy przez macierz
Macierz możemy pomnożyć przez inną macierz, w tym macierz kolumnową albo wierszową. Jeżeli mnożymy macierz A przez macierz B to liczba kolumn A musi być równa liczbie wierszy B. Macierz wynikowa będzie miała tyle wierszy ile ma macierz A i tyle kolumn ile ich miała macierz B. Mnożenie macierzy na ogół nie jest przemienne. Mnożąc A x B otrzymamy inny wynik niż mnożąc B x A. Mnożenie w jednej kolejności może być wykonalne, a w drugą stronę nie. Jeśli jest wykonalne zmianie może ulec wymiar wyniku. Mnożenie macierzy jest przemienne jedynie dla niektórych macierzy kwadratowych.
![]()
Pomnóżmy przez siebie dwie macierze:
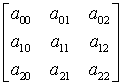 ×
×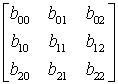 =
=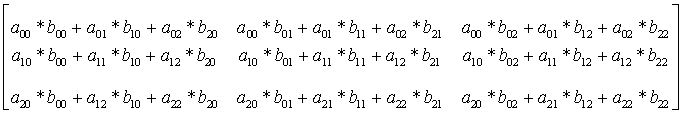
Jeżeli przypomnimy sobie mnożenie skalarne wektorów i potraktujemy pierwszą tablicę jako trzy wektory wierszowe, a drugą tablicę jako trzy wektory kolumnowe, to:
- pierwszy wiersz macierzy wynikowej to trzy iloczyny skalarne pierwszego wektora a przez kolejne wektory b
- drugi wiersz macierzy wynikowej to trzy iloczyny skalarne drugiego wektora a przez kolejne wektory b
- trzeci wiersz macierzy wynikowej to trzy iloczyny skalarne trzeciego wektora a przez kolejne wektory b
Zauważmy, że mnożymy A x B, ale zaczynamy od prawej strony, czyli od B.
Jeżeli mnożone macierze mają różne wielkości musimy najpierw sprawdzić dopuszczalność mnożenia:
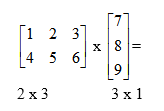
Ponieważ liczba kolumn w pierwszej macierzy = 3 i liczba wierszy w drugiej macierzy = 3 mnożenie jest wykonalne. Wynik będzie postaci 2 x 1.
=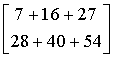 =
=![]()
Dokonajmy odwrotnego mnożenia:
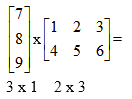
Ponieważ liczba kolumn w pierwszej macierzy = 1, a liczba wierszy w drugiej macierzy = 2 mnożenia nie można wykonać.
Pomnóżmy:
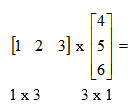
Mnożenie jest wykonalne. Wynik jest postaci 1 x 1, czyli jest to skalar.
![]()
Pomnóżmy:
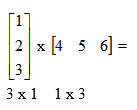
Mnożenie jest wykonalne. Wynik jest postaci 3 x 3.
=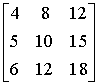
Jeśli mnożymy macierz A przez macierz jednostkową I, to jest to równoznaczne z mnożeniem przez 1 w zwykłej
algebrze, czyli macierz A nie ulega zmianie. Mnożenie takie jest przemienne, tzn. może być wykonywane w dowolnej kolejności:
AI = IA = A
Mnożenie macierzy w języku Java możemy wykonać przy pomocy metod multiply(Matrix) i multiply2(Matrix) z klasy Matrix.
public void multiply(Matrix n) {
double[][] temp = new double[getRowCount()][n.getColCount()];
for (int i = 0; i < getRowCount(); i++) {//2
for (int j = 0; j < n.getColCount(); j++) {//2
for (int k = 0; k < getColCount(); k++) {//3
try {
temp[i][j] += getCell(i, k) * n.getCell(k, j);
} catch (MatrixException e) {
e.printStackTrace();
}
}
}
}
this.setArray(temp);
}
public Matrix multiply2(Matrix n) {
double[][] temp = new double[getRowCount()][n.getColCount()];
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < n.getColCount(); j++) {
for (int k = 0; k < getColCount(); k++) {
try {
temp[i][j] += getCell(i, k) * n.getCell(k, j);
} catch (MatrixException e) {
e.printStackTrace();
}
}
}
}
return new Matrix(temp);
}
Klasa Matrix017
double[] array1 = {1, 2, 3, 4, 5, 6, 7, 8, 9};
Matrix matrix1 = new Matrix(array1, 3);
ArrayUtil.print(array1);
double[] array2 = {9, 8, 7, 6, 5, 4, 3, 2, 1};
Matrix matrix2 = new Matrix(array2, 3);
ArrayUtil.print(array2);
matrix1.multiply(matrix2);
matrix1.printToConsole();
Po uruchomieniu otrzymujemy na konsoli:
[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0] [9.0, 8.0, 7.0, 6.0, 5.0, 4.0, 3.0, 2.0, 1.0] 30.0 24.0 18.0 84.0 69.0 54.0 138.0 114.0 90.0
Klasa Matrix018
double[] array1 = {2, 0, 0, 0, 2, 0, 0, 0, 2};
Matrix matrix1 = new Matrix(array1, 3);
ArrayUtil.print(array1);
double[] array2 = {3, 0, 0, 0, 3, 0, 0, 0, 3};
Matrix matrix2 = new Matrix(array2, 3);
ArrayUtil.print(array2);
matrix1.multiply(matrix2);
matrix1.printToConsole();
boolean a = false;
double[] diagonals = matrix2.getDiagonal();
ArrayUtil.print(diagonals);
try {
a = matrix2.isScalarMatrix();
} catch (MatrixException e) {
e.printStackTrace();
}
Util.print(a);
Po uruchomieniu otrzymujemy na konsoli:\
[2.0, 0.0, 0.0, 0.0, 2.0, 0.0, 0.0, 0.0, 2.0] [3.0, 0.0, 0.0, 0.0, 3.0, 0.0, 0.0, 0.0, 3.0] 6.0 0.0 0.0 0.0 6.0 0.0 0.0 0.0 6.0 [3.0, 3.0, 3.0] true
Mnożenie macierzy przez macierz skalarną
Pomnożenie macierzy przez macierz skalarną jest równoznaczne pomnożeniu tej macierzy przez skalar α.
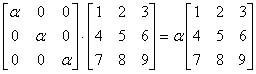
Macierze skalarne dodaje się przez dodawanie skalarów:
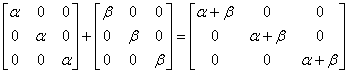
Macierze skalarne mnoży się przez pomnożenie skalarów:
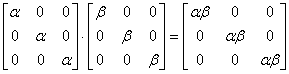
Klaa Matrix009
double[] array1 = {2, 0, 0, 0, 2, 0, 0, 0, 2};
Matrix matrix1 = new Matrix(array1, 3);
ArrayUtil.print(array1);
double[] array2 = {3, 0, 0, 0, 3, 0, 0, 0, 3};
Matrix matrix2 = new Matrix(array2, 3);
ArrayUtil.print(array2);
matrix1.multiply(matrix2);
matrix1.printToConsole();
boolean a = false;
double[] diagonals = matrix2.getDiagonal();
ArrayUtil.print(diagonals);
try {
a = matrix2.isScalarMatrix();
} catch (MatrixException e) {
e.printStackTrace();
}
Util.print(a);
Po uruchomieniu na konsoli zobaczymy:
[2.0, 0.0, 0.0, 0.0, 2.0, 0.0, 0.0, 0.0, 2.0] [3.0, 0.0, 0.0, 0.0, 3.0, 0.0, 0.0, 0.0, 3.0] 6.0 0.0 0.0 0.0 6.0 0.0 0.0 0.0 6.0 [3.0, 3.0, 3.0] true
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 009;

