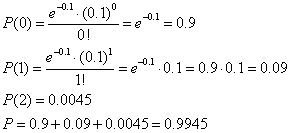Wzór Poissona
Obliczamy prawdopodobieństwo liczby k sukcesów w n-elementowej próbie. Korzystamy z wzoru Poissona
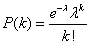
gdzie
n jest liczebnością próby
k jest zakładaną liczbą sukcesów
p jest prawdopodobieństwem zdarzenia sprzyjającego
λ = n × p
e jest liczbą Eulera = 2.718
Wzór Poissona jest stosowany gdy:
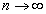
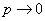
- Iloczyn λ = np jest wielkością stałą
- λ > 0
Przy stosowaniu wzoru n powinno być większe od 99, a λ < 21
Przykład 1
Zakładamy, że każda osoba cywilna spotkana z bronią na ulicy jest terrorystą. Prawdopodobieństwo p napotkania terrorysty wynosi 0.0001.
Policja rewiduje 1000 losowo wybranych osób. Jakie jest prawdopodobieństwo, że wśród tych osób będzie 2 terrorystów?
n = 1000
p = 0.0001
λ = n x p = 1000 x 0.0001 = 0.1
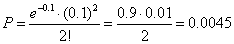
Przykład 2
Jakie jest prawdopodobieństwo, że w warunkach Przykładu 1 w badanej próbie znajdzie się
co najwyżej (nie więcej niż) dwóch terrorystów.
Badane prawdopodobieństwo jest sumą trzech prawdopodobieństw:
- P(0) = nie zostanie złapany żaden terrorysta
- P(1) – zostanie złapany 1 terrorysta
- P(2) – zostanie złapanych 2 terrorystów