Wyznacznik macierzy (Java) (3)

Wyznacznik macierzy (Java) (3)

Twierdzenie Cauchy’ego

Jeżeli dwie macierze są tego samego stopnia to wyznacznik iloczynu macierzy równa się iloczynowi wyznaczników:

czyli mówiąc krócej, zamiast mnożyć macierze i obliczać wyznacznik, można obliczyć i pomnożyć wyznaczniki.

Jeżeli

Obliczenia wykonane są w klasie Matrix053.

Po uruchomieniu klasy na konsoli zobaczymy:

[1.0, 3.0, -2.0, 7.0]
[-3.0, 0.0, 2.0, -1.0]
3.0 -3.0
20.0 -7.0
39.0

Algorytm Gaussa

Opracowując swój algorytm Gauss wziął pod uwagę właściwości wyznacznika. Najlepiej pokazać to na przykładzie.

Mamy macierz wyjściową:

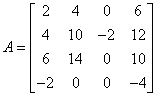
Macierz jest kwadratowa. Nie ma żadnej kolumny, ani wiersza zerowego. Gdyby miała – wyznacznik byłby równy 0. Macierz jest nieosobliwa, a zatem ma wyznacznik różny od zera (Klasa Matrix052).

2.0 4.0 0.0 6.0
4.0 10.0 -2.0 12.0
6.0 14.0 0.0 10.0
-2.0 0.0 0.0 -4.0
144.0

Wyznacznik obliczony metodą Laplace’a wynosi 144.

Pierwszy element a₁₁ macierzy jest różny od zera. Gdyby był równy zero, należałoby zamienić ten wiersz z innym wierszem, którego pierwszy element nie jest zerowy. Przy takiej zamianie należy pamiętać, że znak wyznacznika zmienił się na przeciwny.

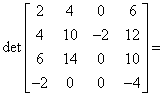
Od drugiego wiersza odejmujemy podwojony wiersz pierwszy:

i otrzymujemy:

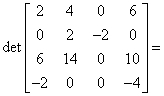
Od wiersza trzeciego odejmujemy potrojony wiersz pierwszy:

i otrzymujemy:

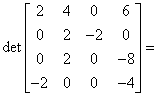
Do wiersza czwartego dodajemy wiersz pierwszy:

i otrzymujemy:

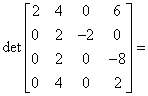
Celem wszystkich operacji było wyzerowanie wszystkich elementów w kolumnie poza elementem pierwszym. Gdyby wiersze były ułożone odmiennie trzeba by czasami dokonać dzielenia zamiast mnożenia.

Zauważmy, że

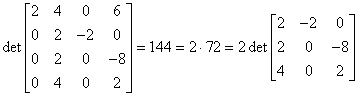
Od wiersza trzeciego odejmujemy wiersz drugi:

i otrzymujemy:

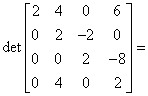
Od wiersza 4 odejmujemy podwojony wiersz drugi:

i otrzymujemy:

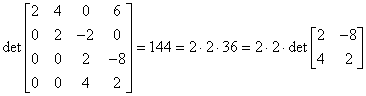
Od wiersza 4 odejmujemy podwojony wiersz trzeci:

i otrzymujemy:

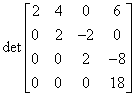
Zauważmy, że:

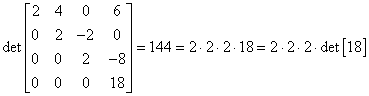
czyli w skrócie:

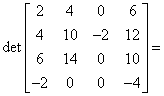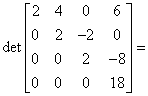==2⋅2⋅2⋅18=144

Macierz została przekształcona w macierz górnotrójkątną, a wyznacznik macierzy jest iloczynem wartości leżących na głównej przekątnej. Identycznie można przekształcić macierz w macierz dolnotrójkątną. Dzielenia można używać, gdy jest to niezbędne. Powyżej nie używaliśmy dzielenia, aby nie ‘zaciemniać’ algorytmu.

Faktyczne obliczanie odbywa się następująco:

Ponieważ a₁₁ jest dzielnikiem dlatego nie może być zerem

W przypadku konieczności dokonania zamiany wierszy należy pamiętać o zmianie znaku wyznacznika.

Analogiczne operacje można wykonywać na kolumnach, ale jak przekonamy się dalej, w wielu algorytmach (np. rozwiązywanie równań liniowych) dozwolone są wyłącznie operacje na wierszach, dlatego nie przedstawiamy tutaj stosownych przykładów.

Możemy też użyć poniższej detGauss(Matrix). O operacjach T i E wykonywanych w tym algorytmie opowiem przy omawianiu metody eliminacji Gaussa.

Obliczenia przeprowadzimy w klasie Matrix068:

  double[][] array = {{2, 4, 0, 6}, {4, 10, -2, 12}, {6, 14, 0, 10},
                {-2, 0, 0, -4}};
        Matrix matrix = new Matrix(array);
        matrix.printToConsole();
        Util.print("");
        if (matrix.isSquareMatrix()) {
            try {
                Util.print(matrix.det());
            } catch (MatrixException e) {
                e.printStackTrace();
            }
        }
        Matrix matrix1 = MatrixUtil.elimGauss(matrix);
        matrix1.printToConsole();
        double det = MatrixUtil.detGauss(matrix);
        Util.print(det);

Po uruchomieniu klasy otrzymujemy na konsoli:

2.0 4.0 0.0 6.0
4.0 10.0 -2.0 12.0
6.0 14.0 0.0 10.0
-2.0 0.0 0.0 -4.0
144.0
2.0 4.0 0.0 6.0
0.0 2.0 -2.0 0.0
0.0 0.0 2.0 -8.0
0.0 0.0 0.0 18.0
144.0

Jak widzimy wyznacznik obliczony metodą klasyczną i wyznacznik obliczony metodą eliminacji Gaussa są identyczny.

Zastosowania wyznacznika

Wyznaczniki są wykorzystywane:

1. przy rozwiązywaniu równań liniowych
2. przy odwracaniu macierzy
3. w geometrii analitycznej przy obliczaniu objętości brył
4. w badaniu niektórych wielomianów
5. w analizie matematycznej przy zamianie zmiennych w całkach wielokrotnych
6. etc.

Pliki do ściągnięcia

matrices013.zip

Moduł matrices – aktualny stan projektu = 013;

2019-11-17 15:12:56