
Wyznacznik macierzy (Java) (2)
Geometryczna interpretacja wyznacznika
Użyjemy klasy Matrix020
Po uruchomieniu kodu na konsoli zobaczymy:
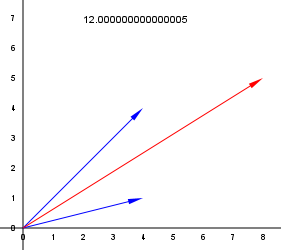
Załóżmy, że mamy dwa wektory V1=[4,4] i V2= [4,1]. Jeżeli narysujemy je na płaszczyźnie i narysujemy wektor będący sumą tych wektorów to otrzymamy równoległobok, którego dłuższą przekątną jest wektor oznaczony na czerwono będący suma tych dwóch wektorów. Pole równoległoboku to:
S = a*b*sinα
gdzie:
S – pole równoległoboku
a – jest długością pierwszego wektora (I bok równoległoboku),
b – jest długością drugiego wektora (II bok równoległoboku),
α jest kątem między wektorami
W naszym przykładzie S = 12.
det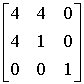 = 4⋅1 – 4⋅4 = -12, |det| = 12
= 4⋅1 – 4⋅4 = -12, |det| = 12
Jak widzimy wyznacznik macierzy jest równy polu równoległoboku rozpiętego na płaszczyźnie na tych wektorach.
Jeżeli obliczymy wektor 2d, który jest iloczynem wektorowym obu podanych wektorów to jego długość będzie równa 12 (Klasa Matrix021):
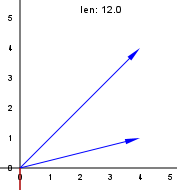
Jeżeli obliczymy wektor 3d, który jest iloczynem wektorowym obu podanych wektorów z częścią z = 0, to długość tego wektora będzie wynosiła 12.
Jeżeli macierz będzie miała trzy ‘pełne’ wektory to wyznacznik macierzy 3 x 3 będzie objętością równoległościanu rozpiętego w przestrzeni na tych 3 wektorach.
Jeżeli weźmiemy trzy wektory V1=[a,b], V2=[c,d], V3 =[g,h] i narysujemy je na płaszczyźnie to pole S trójkąta wyznaczonego przez końce tych wektorów wynosi:
S = ![]() det
det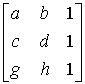 = (ad1 + b1g + 1ch) – (1dg + a1h + bc1) =
= (ad1 + b1g + 1ch) – (1dg + a1h + bc1) =
= (ad + bg + ch) – (dg + ah + bc)
Jeżeli nasz trójkąt to: V1=[1,-1], V2=[3,4], V3=[-2,5]
det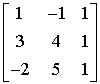 = (4 + 2 + 15)-(-8+5-3) = 21 -(-6)=21+6=27;
= (4 + 2 + 15)-(-8+5-3) = 21 -(-6)=21+6=27;
pole S= ![]() ⋅27 = 13.5
⋅27 = 13.5
Po uruchomieniu klasy Matrix022 zobaczymy:
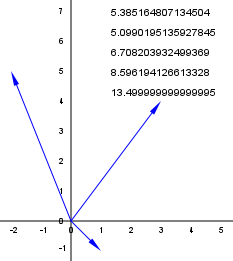
Z geometrii wynika, że boki trójkąta wynoszą:
x = Math.sqrt((a-c)2+(b-d)2) = Math.sqrt((1-3)2+(-1-4)2) = Math.sqrt(4+25) = 5.385,
y = Math.sqrt((c-g)2+(d-h)2) = Math.sqrt((3+2)2+(4-5)2) = Math.sqrt(25+1)=5.099,
z = Math.sqrt((g-a)2+(h-b)2) = Math.sqrt((-2-1)2+(5+1)2)= Math.sqrt(9+36)=6.708,
Połowa obwodu p = (x + y + z)/2 = 5.385+5.099+6.708 = 17.192/2 = 8.596
![]() =
= ![]() =
= ![]() =
= ![]() = 13.499
= 13.499
Możemy to też obliczyć używając iloczynu skalarnego:
Obliczamy iloczyny skalarne V1xV2, V2xV3, V3xV1. Obliczamy połowy długości tych wektorów. Dodajemy długości dwóch pierwszych i odejmujemy trzecią. Wynik jest dokładnie 13.5.
Jeżeli obliczenia przeprowadzimy przy użyciu klasy Matrix021 zobaczymy cos takiego:

Wyznacznik macierzy n × n
Rozwinięcie Laplace’a
Najlepszą metodą wyznaczania wyznacznika jest metoda Laplace’a (rozwinięcie Laplace’a).
Wyznacznik macierzy kwadratowej stopnia oblicza się z następującego wzoru:
![]()
gdzie:
i – jest ustalone i jest wybranym numerem wiersza, względem którego następuje rozwinięcie.
![]() – jest elementem macierzy w i-tym wierszu i j-tej kolumnie.
– jest elementem macierzy w i-tym wierszu i j-tej kolumnie.
![]() – jest dopełnieniem algebraicznym elementu
– jest dopełnieniem algebraicznym elementu ![]() (czyli jest to iloczyn minoru elementu
(czyli jest to iloczyn minoru elementu ![]() pomnożony przez czynnik
pomnożony przez czynnik ![]()
Powyższe rozważania są słuszne również dla wybranej kolumny.
Tej metody możemy użyć rekurencyjnie dla macierzy o dowolnej wielkości, za każdym razem sprowadzając macierz do niższego stopnia, aż dojdziemy do macierzy takiego stopnia, dla którego jesteśmy w stanie obliczyć wyznacznik.
Przykład
Mamy macierz:
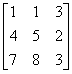
Nasze i=2 czyli wybieramy wiersz 2. Gdyby był jakiś wiersz zawierający 0 lepiej byłoby wybrać właśnie ten wiersz, gdyż zmniejsza to liczbę obliczeń. Będziemy mieli do czynienia z trzema elementami:
![]() = {4,5,2}
= {4,5,2}
Obliczenia dla a21
Z macierzy wybieramy podmacierz dla elementu a21 czyli podmacierz powstałą przez skreślenie drugiego rzędu i pierwszej kolumny:
![]()
Obliczamy wyznacznik, czyli minor tej podmacierzy:
det=-21
Mnożymy ten wyznacznik przez czynnik dopełniający:
![]()
Mnożymy wynik przez wartość elementu:
a1= 4⋅21=84
Obliczenia dla a22
Z macierzy wybieramy podmacierz dla elementu a22 czyli podmacierz powstałą przez skreślenie drugiego rzędu i drugiej kolumny:
![]()
Obliczamy wyznacznik, czyli minor tej podmacierzy:
det=-18
Mnożymy ten wyznacznik przez czynnik dopełniający:
![]()
Mnożymy wynik przez wartość elementu:
![]()
Obliczenia dla a23
Z macierzy wybieramy podmacierz dla elementu a23 czyli podmacierz powstałą przez skreślenie drugiego rzędu i trzeciej kolumny:
![]()
Obliczamy wyznacznik, czyli minor tej podmacierzy:
det=1
Mnożymy ten wyznacznik przez czynnik dopełniający:
![]()
Mnożymy wynik przez wartość elementu:
![]()
Obliczenia wspólne
![]()
Możemy je przeprowadzić używając klasy Matrix050.
Po uruchomieniu klasy na konsoli zobaczymy wynik:
1.0 1.0 3.0 4.0 5.0 2.0 7.0 8.0 3.0 -8.0
Właściwości wyznacznika
- Jeżeli kolumna macierzy lub wiersz macierzy zawierają same 0, to wyznacznik macierzy wynosi 0
- Jeżeli zamienimy miejscami dwa wiersze (albo dwie kolumny) to wyznacznik zmieni swój znak ( + na – albo – na +)
- Jeżeli dwie kolumny (albo dwa wiersze) macierzy są jednakowe to wyznacznik tej macierzy wynosi 0
- Jeżeli wszystkie elementy pewnego wiersza (albo kolumny) zawierają wspólny czynnik, to czynnik ten można wyłączyć przed wyznacznik
- Jeżeli każda z komórek macierzy zawiera wspólny czynnik to czynnik ten po podniesieniu do potęgi równej ilości rzędów (kolumn) można wyłączyć przed wyznacznik
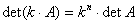
- Jeżeli do elementów dowolnej kolumny (albo wiersza) dodamy odpowiadające im elementy innej kolumny (wiersza) pomnożone przez dowolną liczbę (również 1) to wartość wyznacznika pozostanie nie zmieniona
- Wyznaczniki macierzy i jej macierzy transponowanej są jednakowe
- Wyznacznik macierzy górnotrójkątnej, dolnotrójkątnej lub diagonalnej jest równy iloczynowi elementów na głównej przekątne
- Wyznacznik macierzy odwrotnej jest równy odwrotności wyznacznika
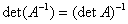
Ad. 1
det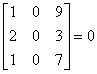
Ad. 2
det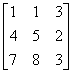 = -8
= -8
det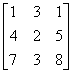 = 8
= 8
Ad. 3
det = 0
= 0
Ad. 4
det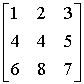 =
= 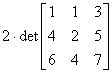
Ad. 5
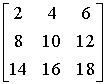 =
= 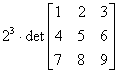
Ad. 6
det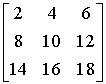 = det
= det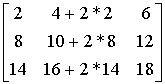
Ad. 7
![]()
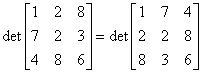
Ad. 8
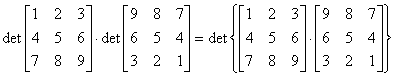
Ad. 9
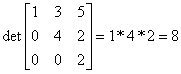
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 012;

