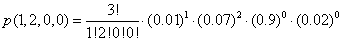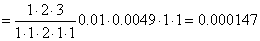Uogólniony wzór Bernoulliego
Wzór Bernoulliego można uogólnić:
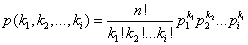
gdzie
p oznacza prawdopodobieństwo
k1, k2, …, ki – oznacza liczbę zdarzeń
sprzyjających.
p1, p2, …, pi – oznacza prawdopodobieństwa
zdarzeń sprzyjających.
n = k1 + ki + … + ki – jest łączną liczbą przeprowadzonych doświadczeń.
p1 + p2 + … + pi = 1
Przykład 1
Wiadomo, że rozkład kolorów oczu jest następujący:
- niebieskie – 7%
- zielone – 1%
- brązowe – 90%
- szare – 2 %
Sprawdzamy kolor oczu trzech osób przypadkowo spotkanych na ulicy osób. Jakie jest prawdopodobieństwo, że 1 osoba będzie miała oczy zielone, a 2 osoby oczy niebieskie?
Rozwiązanie
k1 = 1, p1 = 0.01
k2 = 2, p1 = 0.07
k3 = 0, p1 = 0.90
k4 = 0, p1 = 0.02
n = k1 + k2 + k3+ k4= 1 + 2 + 0 + 0 = 3
p1 +p2+p3+p4 = 0.01 + 0.07 + 0.90 + 0.02 = 1