
System sześćdziesiętny (3)
Obliczanie odwrotności
Wykorzystuje się tablicę ułamków
Dla danej liczby c (igum) trzeba znaleźć odwrotność 1/c = c-1 (igibum).
Algorytm
Używano algorytmu:
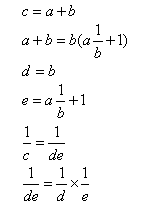
Zadanie praktyczne
| Lp. | Krok algorytmu | Transkrypcja | Komentarz |
|---|---|---|---|
| 1 | [2;13,20] jest igum. Jakie jest igigum? | 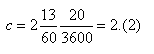 |
|
| 2 | Utwórz odwrotność |
Mamy [2;10] i [;3,20]. Utwórz odwrotność [;3,20], Wynik jest [18]. |
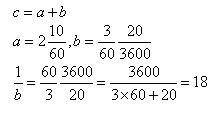 |
| 3 | pomnóż przez |
[18] pomnóż przez [2,10]. Znajdujesz [39]. | 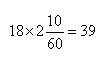 |
| 4 | Dodaj |
Dodaj [1]. Znajdujesz [40]. | |
| 5 | Utwórz odwrotność |
Utwórz odwrotność [40]. Znajdujesz [1;30]. | 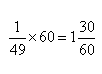 |
| 6 | pomnóż przez | [1;30] pomnóż przez [18]. Znajdujesz [27] | 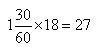 |
| 7 | Igibum jest |
Igibum jest [27] | 27 |
Przekątna kwadratu
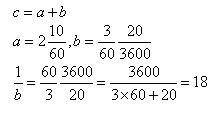

Tabliczka klinowa (fot. unknown)
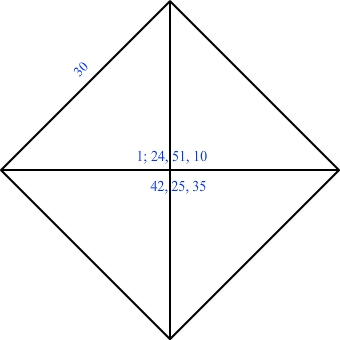
30 = bok kwadratu = a
![]()
![]()
![]()
Przekątna kwadratu według obliczenia ówczesnego: 42.426
Przekątna obliczona według dzisiejszej wartości pierwiastka: 42.426
Dzięki użyciu współczynników proporcjonalności można było szybko obliczyć przekątną dowolnego kwadratu.
Jeśli bok kwadratu wynosił np. 45 = 30x 1.5 wystarczyło pomnożyć wynik dla 30 przez 1.5. Przekątna = 63.6396.
Pierwiastki kwadratowe
| Lp. | Krok algorytmu | Komentarz |
|---|---|---|
| 1 | Dodałem pole i dwie trzecie boku kwadratu i otrzymałem liczbę [0;35]. Jaki jest bok kwadratu? | 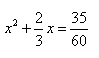 |
| 2 | Bierzesz współczynnik 1. Dwie trzecie ze współczynnika 1 stanowi [0;40]. |
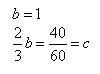 |
| 3 | Połowę z tego [0;20] mnożysz przez [0;20] i otrzymujesz [0;6,40]. |
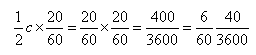 |
| 4 | Dodajesz [0;6,40] do [0;35] i otrzymujesz [0;41;40], które ma [0;50] jako pierwiastek kwadratowy. |
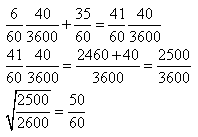 |
| 5 | [0;20], które pomnożyłeś przed siebie, odejmujesz od [0;50] i [0;30] jest bokiem kwadratu. |
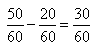 |
| 6 | Bok kwadratu wynosi [0;30]. | Bok kwadratu x=1/2 |

