
Rodzaje macierzy (Java)
Istnieje wiele rodzajów macierzy, które nie są wymienione poniżej. Być może zostaną uwzględnione w dalszej przyszłości.
Macierz kwadratowa
Macierz kwadratowa to macierz, która ma jednakową liczbę wierszy i kolumn.
Macierzy o postaci:
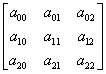
w języku Java odpowiada tablica array[3][3].
Elementy macierzy podaje się w postaci ![]() , gdzie i oznacza numer rzędu, a j numer kolumny, na przecięciu których znajduje się element, a więc element a00 w tablicy byłby elementem
, gdzie i oznacza numer rzędu, a j numer kolumny, na przecięciu których znajduje się element, a więc element a00 w tablicy byłby elementem array[0][0], czyli element leży w pierwszym rzędzie i w pierwszej kolumnie.
Poniższa metoda służy do badania czy macierz jest kwadratowa:
public boolean isSquareMatrix() {
return getRowCount() == getColCount();
}
Macierz zerowa
Macierz zerowa, oznaczana literą Θ (theta), to macierz której wszystkie elementy są równe 0. Macierz można wyzerować używając metody setToValue(). Przykład podany był w pliku Matrix001.java
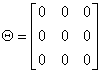
Czy macierz jest zerowa możemy sprawdzić przy użyciu metody:
public boolean isZeroMatrix() {
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if (array[i][j] != 0.0) {
return false;
}
}
}
return true;
}
Macierz jednostkowa
Macierz diagonalną, której wszystkie elementy leżące na tzw. głównej przekątnej są równe 1, a pozostałe są równe 0, nazywana jest macierzą jednostkową:
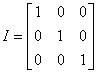
W algebrze macierzy mnożenie przez macierz jednostkową jest odpowiednikiem mnożenia przez 1.
![]()
![]()
Macierz możemy uczynić jednostkową używając metody:
public void setToIdentity() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if (i == j) {
array[i][j] = 1.0;
} else {
array[i][j] = 0.0;
}
}
}
}
Sprawdzić, czy macierz jest jednostkowa, możemy przy uzyciu poniższej metody:
public boolean isIdentityMatrix() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if ((i != j) && (array[i][j] != 0)) {
return false;
} else if ((i == j) && (array[i][j] != 1)) {
return false;
}
}
}
return true;
}
Klasa Matrix008.java
1 package matrices2; 2 3 import matrices.Matrix; 4 import matrices.MatrixException; 5 6 public class Matrix008 { 7 public static void main(String[] args) { 8 Matrix matrix = new Matrix(3, 3); 9 try { 10 matrix.setToIdentity(); 11 } catch (MatrixException e) { 12 e.printStackTrace(); 13 } 14 matrix.printToConsole(); 15 try { 16 System.out.println(matrix.isIdentityMatrix()); 17 } catch (MatrixException e) { 18 e.printStackTrace(); 19 } 20 } 21 } 22
Po uruchomieniu klasy na konsoli zobaczymy:
1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0 true
Macierz elementarna
Zostanie omówiona w oddzielnym wpisie.
Macierze przekształceń elementarnych
Zostaną omówione w oddzielnym wpisie.
Macierz wierszowa
Macierz ![]() , która posiada tylko jeden wiersz jest nazywana macierzą wierszową albo wektorem wierszowym:
, która posiada tylko jeden wiersz jest nazywana macierzą wierszową albo wektorem wierszowym:
![]()
Przy użyciu poniższej metody można sprawdzić czy badana macierz jest macierzą wierszową:
public boolean isRowMatrix() {
return getRowCount() == 1;
}
Macierz kolumnowa
Macierz ![]() , która ma tylko jedną kolumnę nazywana jest macierzą kolumnową albo wektorem kolumnowym:
, która ma tylko jedną kolumnę nazywana jest macierzą kolumnową albo wektorem kolumnowym:
![]()
Przy użyciu poniższej metody możemy sprawdzić czy macierz jest macierzą kolumnową:
public boolean isColumnMatrix() {
return getColCount() == 1;
}
Macierz diagonalna
Macierz diagonalna to macierz kwadratowa, której wszystkie elementy, poza elementami leżącymi na przekątnej, są równe 0.
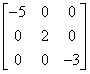
Taką macierz można też zapisać jako:
![]()
Właściwości macierzy diagonalnych
- Suma macierzy diagonalnych jest macierzą diagonalną
- Iloczyn macierzy diagonalnych jest macierzą diagonalną
- Podniesienie każdego z elementów diagonalnych do potęgi n oznacza podniesienie całej macierzy do tej potęgi
- Wyznacznik macierzy diagonalnej jest iloczynem elementów diagonalnych
- Jeżeli wyznacznik macierzy jest odwracalny, to macierz jest nieosobliwa
- Macierz jest odwracalna jeśli każdy jej element jest odwracalny. Macierz odwracamy przez odwrócenie każdego jej elementu
Ad. 2
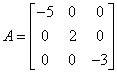
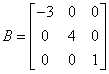
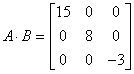
Ad. 3
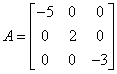
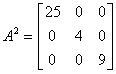
Ad. 4
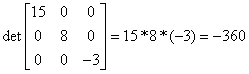
Ad. 6
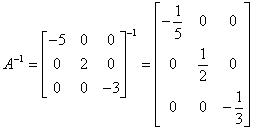
Metody
Aby sprawdzić czy macierz jest diagonalna możemy użyć metody:
public boolean isDiagonalMatrix() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if ((array[i][j] != 0.0) && (i != j)) {
return false;
}
}
}
return true;
}
Elementy leżące na przekątnej możemy pobrać do tablicy przy użyciu metody:
public double[] getDiagonal() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
int len = getRowCount();
double[] diagonals = new double[len];
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if (i == j) {
diagonals[i] = getArray()[i][j];
}
}
}
return diagonals;
}
Macierz skalarna
Jest macierzą diagonalną, której każdy element jest wartością skalarną α.
Jeżeli ![]()
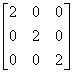
Jest iloczynem macierzy jednostkowej I przez skalar:
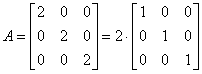
Czy macierz jest skalarna możemy sprawdzić przy użyciu metody:
public boolean isScalarMatrix() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
double[] diagonals = getDiagonal();
double first = diagonals[0];
for (int i = 1; i < diagonals.length; i++) {
if (diagonals[i] != first) {
return false;
}
}
return true;
}
Macierz symetryczna
Macierz symetryczna to macierz, której elementy rozmieszczone symetrycznie po obu stronach przekątnej głównej są równe, czyli
![]()
Przy transpozycji (opowiem o niej oddzielnie) otrzymujemy tę samą macierz:
![]()
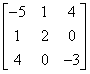
Czy macierz jest symetryczna można sprawdzić przy użyciu metody:
public boolean isSymmetricMatrix() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if (array[i][j] != array[j][i]) {
return false;
}
}
}
return true;
}
Macierz antysymetryczna
Macierz antysymetryczna to taka macierz, w której elementy rozmieszczone symetrycznie po obu stronach przekątnej głównej są przeciwne (mają przeciwne znaki), czyli:
![]()
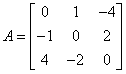
Z warunku wynika, że elementy diagonalne muszą być równe 0.
W procesie transpozycji ![]()
Czy macierz jest antysymetryczna można sprawdzić przy użyciu metody:
public boolean isAntisymmetricMatrix() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if (array[i][j] != -array[j][i]) {
return false;
}
}
}
return true;
}
Macierz trójdiagonalna
Macierz jest trójdiagonalna jeżeli wszystkie elementy macierzy leżące poza główną przekątną i dwiema przylegającymi do niej przekątnymi są zerowe.
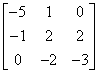
Czy macierz jest trójdiagonalna można sprawdzić przy użyciu poniższej metody:
public boolean is3DiagonalMatrix() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
for (int i = 0; i <getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if ((array[i][j] == 0.0) && !(Math.abs(i - j) > 1)) {
return false;
}
}
}
return true;
}
Macierz górnotrójkątna
Macierz górnotrójkątna to macierz, której elementy leżące poniżej przekątnej głównej są zerowe.
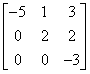
Macierz wynikowa z pomnożenia przez siebie 2 macierzy górnotrójkątnych jest macierzą górnotrójkątną.
Czy macierz jest górnotrójkątna można sprawdzic przy użyciu poniższej metody:
public boolean isUpperTriangleMatrix() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if ((i > j) && (array[i][j] != 0)) {
return false;
}
}
}
return true;
}
Macierz dolnotrójkątna
Macierz dolnotrójkątna to macierz, której elementy leżące powyżej przekątnej głównej są zerowe.
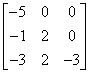
Macierz wynikowa z pomnożenia przez siebie 2 macierzy dolnotrójkątnych jest macierzą dolnotrójkątną.
Czy macierz jest dolnotrójkątna możemy sprawdzić przy użyciu poniższej metody:
public boolean isLowerTriangleMatrix() throws MatrixException {
if (!isSquareMatrix()) {
throw new MatrixException("Macierz nie jest kwadratowa");
}
for (int i = 0; i < getRowCount(); i++) {
for (int j = 0; j < getColCount(); j++) {
if ((i < j) && (array[i][j] != 0)) {
return false;
}
}
}
return true;
}
Podmacierz
Podmacierz to macierz powstała z macierzy przez usunięcie z niej dowolnej liczby wierszy i/lub kolumn niekoniecznie do siebie przylegających. Indeksy podmacierzy zaczynają się od 1.
Macierz 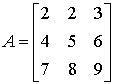
Podmacierz 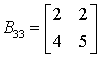
Metody
Podmacierz możemy znaleźć używając metod:
public static Matrix submatrix(Matrix matrix, int row, int col) {
Matrix mat1 = deleteRow(matrix, row);
return deleteCol(mat1, col);
}
// w tablicach podane są indeksy kolumn do usunięcia
public static Matrix submatrix(Matrix matrix, int[] rows, int[] cols) {
Matrix mat = null;
try {
mat = matrix.clone();
} catch (CloneNotSupportedException e) {
e.printStackTrace();
}
int ii = 0;
for (int row : rows) {
mat = deleteRow(matrix, row - ii);
ii++;
}
int jj = 0;
for (int col : cols) {
mat = deleteCol(mat, col - jj);
jj++;
}
return mat;
}
//pobiera podmacierz składającą się z podanej liczby rzędów i kolumn
//bezpośrednio do siebie przylegających
public static Matrix submatrix(Matrix matrix, int startRow, int endRow,
int startCol, int endCol) {
int len1 = endRow - startRow + 1;
int len2 = endCol - startCol + 1;
int len = len1 * len2;
double[] ar = new double[len];
int k = 0;
for (int i = startRow; i <endRow + 1; i++) {
for (int j = startCol; j < endCol + 1; j++) {
ar[k] = matrix.getArray()[i][j];
k++;
}
}
return new Matrix(ar, len2);
}
Przykłady
Klasa Matrix019.java
Z podanej macierzy usuwamy 3 wiersz i kolumnę.
double[][] array = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
Matrix matrix = new Matrix(array);
matrix.printToConsole();
Util.print("");
Matrix matrix1 = MatrixUtil.submatrix(matrix, 2, 2);
matrix1.printToConsole();
Po uruchomieniu klasy na konsoli zobaczymy:
1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 1.0 2.0 4.0 5.0
Klasa Matrix028.java
double[] array1 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15,
16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,
32, 33, 34, 35, 36};
Matrix matrix1 = new Matrix(array1, 6);
matrix1.printToConsole();
Matrix matrix2 = MatrixUtil.submatrix(matrix1, 2, 4, 2, 4);
matrix2.printToConsole();
Z macierzy
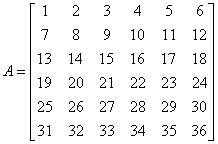
wybieramy podmacierz: 3, 4 i 5 rząd oraz 3, 4 i 5 kolumna. Otrzymujemy podmacierz:
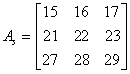
Klasa Matrix055.java
double[][] arr = {{1, 2, 3, 4, 5}, {2, 3, 4, 5, 6}, {3, 4, 5, 6, 7},
{4, 5, 6, 7, 8}};
Matrix mat = new Matrix(arr);
mat.printToConsole();
System.out.println();
Matrix mat1 = MatrixUtil.submatrix(mat, new int[]{1}, new int[]{1, 3});
mat1.printToConsole();
Z macierzy
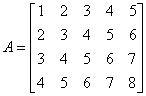
Usuwamy rząd 2 oraz kolumny 2 i 4. Otrzymujemy podmacierz:
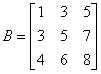
Podmacierz główna
Podmacierz główna, to taka podmacierz, która jeśli zawiera elementy i-tego wiersza macierzy wyjściowej to zawiera również elementy i-tej kolumny tej macierzy.
Macierz:
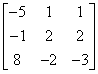
Podmacierz główna (zawiera elementy drugiego wiersza i drugiej kolumny):
![]()
Podmacierzą główną jest również każdy z elementów leżących na przekątnej głównej.
Macierz transponowana
Zostanie omówiona w rozdziale 'Transpozycja macierzy’.
Macierz odwrotna
Zostanie omówiona w rozdziale 'Odwracanie macierzy’.
Macierz osobliwa
Jeżeli wyznacznik macierzy równa się zeru to macierz nie ma odwrotności (jest nieodwracalna) i nazywana jest macierzą osobliwą.
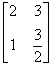
Osobliwość macierzy możemy sprawdzić używając metody:
public boolean isSingularMatrix() {
double det = 0.0;
try {
det = det();
} catch (MatrixException e) {
e.printStackTrace();
}
return det == 0;
}
Klasa Matrix024.java
double[] array = {2, 3, 1, 1.5};
Matrix matrix = new Matrix(array, 2);
matrix.printToConsole();
try {
System.out.println("det: " + matrix.det());
} catch (MatrixException e) {
e.printStackTrace();
}
System.out.println("czy jest osobliwa?: " + matrix.isSingularMatrix());
Sprawdzamy, czy powyższa macierz jest osobliwa. Po uruchomieniu klasy na konsoli zobaczymy:
2.0 3.0 1.0 1.5 det: 0.0 czy jest osobliwa?: true
Macierz nieosobliwa
Jeżeli wyznacznik macierzy jest różny od zera to macierz ma odwrotność (jest odwracalna) i nazywana jest macierzą nieosobliwą.
![]()
Klasa Matrix025.java
Testujemy osobliwość macierzy.
double[] array = {2, 3, 1, 3};
Matrix matrix = new Matrix(array, 2);
matrix.printToConsole();
try {
System.out.println("det: " + matrix.det());
} catch (MatrixException e) {
e.printStackTrace();
}
System.out.println("czy jest osobliwa?: " + matrix.isSingularMatrix());
Po uruchomieniu klasy na konsoli zobaczymy:
2.0 3.0 1.0 3.0 det: 3.0 czy jest osobliwa?: false
Macierz schodkowa
Macierz schodkowa to macierz, w której wiersze zerowe (jeśli występują) znajdują się najniżej, a w wierszach niezerowych, pierwsze niezerowe elementy, kolejnych niezerowych wierszy, znajdują się w coraz dalszych kolumnach.

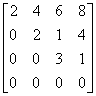
![]()
Macierz schodkowa zredukowana
Macierz schodkowa zredukowana to macierz, która:
- jest schodkowa
- w każdym wierszu niezerowym, pierwszy niezerowy wyraz jest równy 1, a pod nim (w kolumnie) występują wyłącznie zera
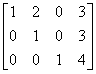
Macierz kwadratowa, w postaci schodkowej zredukowanej jest zawsze macierzą górnotrójkątną.
Macierz ortogonalna
Macierz kwadratowa A jest nazywana macierzą ortogonalną, jeśli macierz transponowana macierzy A pomnożona przez macierz daje w wyniku macierz jednostkową:
![]()
Z tego wynika, że:
![]()
Wyznacznik macierzy ortogonalnej jest równy 1 albo -1.
Mamy macierz:
![]()
![]()
![]()
![]()
Klasa Matrix078.java
double[][] A = {{1, 0}, {0, -1}};
Matrix m = new Matrix(A);
m.printToConsole();
Util.print("");
Matrix m1 = MatrixUtil.transpose(m);
m1.printToConsole();
Util.print("");
Matrix m2 = MatrixUtil.multiply3(m1, m);
m2.printToConsole();
Util.print("");
Matrix m3 = MatrixUtil.inverseGauss(m);
m3.printToConsole();
Util.print("");
Po uruchomieniu klasy na konsoli otrzymujemy:
1.0 0.0 0.0 -1.0 1.0 0.0 0.0 -1.0 1.0 0.0 0.0 1.0 1.0 0.0 0.0 -1.0
Macierz blokowa
Omówiono w podrozdziale poświęconym partycjonowaniu macierzy.
Macierz nilpotentna
Macierz nilpotentna, to macierz kwadratowa, która podniesiona do pewnej potęgi n (gdzie n jest liczbą całkowitą dodatnią) jest macierzą zerową:
![]()
Najniższe n, które spełnia powyższą równość nazywane jest indeksem n.
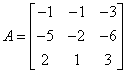
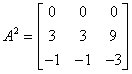
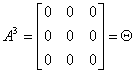
Macierz A jest macierzą nilpotentną o indeksie n=3.
Przykład w klasie Matrix086.java w załączonych plikach.
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 002;

