Partycjonowanie macierzy (Java)

Partycjonowanie macierzy (Java)

Partycjonowanie macierzy oznacza podział macierzy na podmacierze. Powstaje wtedy macierz blokowa. Na ogół partycjonowanie stosuje się przy mnożeniu macierzy, które są zbyt duże aby się pomieścić w pamięci.

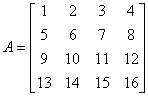
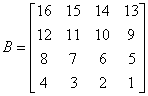
Każdą z macierzy możemy podzielić na partycje.

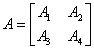
Będzie to wyglądało tak:

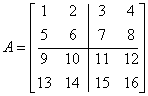
Macierz B również możemy podzielić na partycje:

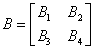
Będzie to wyglądało tak:

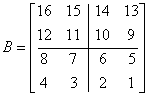
Teraz możemy wykonać mnożenie:

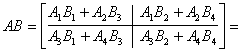
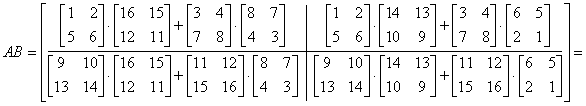
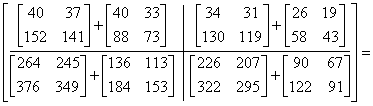
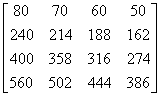
Przykład w klasie Matrix029:

[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0,
  10.0, 11.0, 12.0, 13.0, 14.0, 15.0, 16.0]
[16.0, 15.0, 14.0, 13.0, 12.0, 11.0, 10.0, 9.0,
   8.0, 7.0, 6.0, 5.0, 4.0, 3.0, 2.0, 1.0]
80.0 70.0 60.0 50.0
240.0 214.0 188.0 162.0
400.0 358.0 316.0 274.0
560.0 502.0 444.0 386.0

Podmacierze nie muszą być kwadratowe. Podział musi być tak dokonany, aby macierze dały się pomnożyć zgodnie z regułami mnożenia macierzy. A oto przykład takiego podziału:

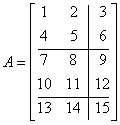
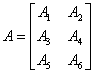
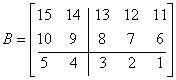
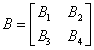
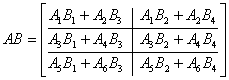
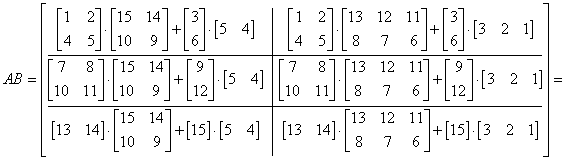
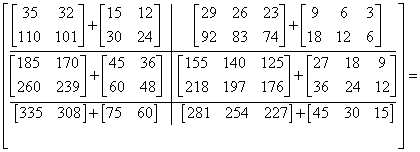
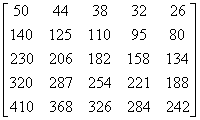
Przykład w klasie Matrix030:

[1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0,
  10.0, 11.0, 12.0, 13.0, 14.0, 15.0]
[15.0, 14.0, 13.0, 12.0, 11.0, 10.0, 9.0, 8.0,
  7.0, 6.0, 5.0, 4.0, 3.0, 2.0, 1.0]
50.0 44.0 38.0 32.0 26.0
140.0 125.0 110.0 95.0 80.0
230.0 206.0 182.0 158.0 134.0
320.0 287.0 254.0 221.0 188.0
410.0 368.0 326.0 284.0 242.0

Jak widzimy macierze stojące w i-tym wierszu macierzy blokowej muszą mieć taką samą liczbę wierszy, a macierze stojące w j-tej kolumnie – taką samą liczbę kolumn.

Macierze diagonalne blokowe

Macierz blokowa diagonalna to macierz, która w wyniku partycjonowania przybiera formę

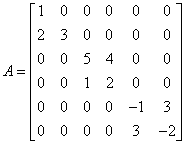jest macierzą diagonalną blokową, gdyż

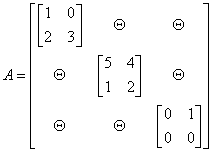
Oczywiście bloki macierzy nie muszą być jednakowej wielkości.

Pliki do ściągnięcia

matrices024.zip

Moduł matrices – aktualny stan projektu = 024;

2019-12-07 07:36:31