Partycje (kombinatoryka) - Blog Zielonego Smoka

Zielony Smok - logo witryny

Partycje

Partycja liczby n jest przedstawieniem liczby n jako sumy liczb naturalnych.

Na ogół rozważa się trzy zagadnienia:

n jako suma dokładnie k liczb naturalnych
n jako suma co najwyżej k liczb naturalnych
n jako suma liczb naturalnych

Pytamy o liczbę partycji.

n jako suma dokładnie k liczb naturalnych

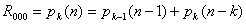, czyli

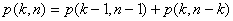
przy czym wiadomo, że:

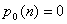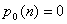
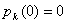, czyli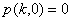

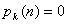, czyli 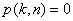, jeżeli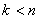

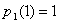, czyli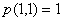

Zadanie:

Na ile sposobów możemy przedstawić liczbę 4 jako sumę 3 liczb naturalnych.

Rozwiązanie:

n=4, k=3

p(1, 1) = 1

p(1, 2) = p(0, 1) + p(1, 1) = 0 + 1 = 1

p(2, 3) = p(1, 2) + p(2, 1) = 1 + 0 = 1

p(3, 4) = p(2, 3) + p(3, 1) = 1 + 0 = 1

1 sposób

Wynik: 1

Sprawdzenie

4 da się zapisać jako suma trzech liczb tylko w jeden sposób: 1 + 1 + 2.

Jest to sposób identyczny z Rozmieszczeniem 1 (R₀₀₀), o którym napiszę wkrótce.

Tabela partycji

Tab. 1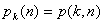

k\n	n=1	2	3	4	5	6	7	8	9	10
k=1	1	1	1	1	1	1	1	1	1	1
2		1	1	2	2	3	3	4	4	5
3			1	1	2	3	4	5	7	8
4				1	1	2	3	5	6	9
5					1	1	2	3	5	7
6						1	1	2	3	5
7							1	1	2	3
8								1	1	2
9									1	1
10										1
p(n)	1	2	3	5	7	11	15	22	30	42

Jeśli weźmiemy n=7, k=2, to z tabeli odczytamy, że liczba 7 da się przedstawić jako suma 2 liczb naturalnych na 3 różne sposoby (1+6, 2+5, 3+4).

n jako suma co najwyżej k liczb naturalnych

Przykład

Na ile sposobów możemy przedstawić liczbę 4 jako sumę co najwyżej 3 liczb naturalnych?

Rozwiązanie

Korzystamy z powyższej tabeli. Sumujemy wyniki z kolumny n = 4 dla k = 1, k = 2 i k = 3

1 + 2 + 1 = 4

Sprawdzenie

4
3 + 1
2 + 2
2 + 1 + 1

n jako suma liczb naturalnych

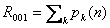
gdzie

, czyli

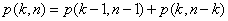
Zadanie:

Na ile sposobów można zapisać liczbę naturalną (np. 4) jako sumę liczb naturalnych, czyli ile istnieje partycji liczby n?

Rozwiązanie:

n=4, k=4

p(1, 1) = 1

p(1, 2) = p(0, 1) + p(1, 1) = 0 + 1 = 1

p(2, 2) = p(1, 1) + p(2, 0) = 1 + 0 = 1

p(1, 3) = p(0, 2) + p(1, 2) = 0 + 1 = 1

p(2, 3) = p(1, 2) + p(2, 1) = 1 + 0 = 1

p(3, 3) = p(2, 2) + p(3, 0) = 1 + 0 = 1

p(1, 4) = p(0, 3) + p(1, 3) = 0 + 1 = 1

p(2, 4) = p(1, 3) + p(2, 2) = 1 + 1 = 2

p(3, 4) = p(2, 3) + p(3, 1) = 1 + 0 = 1

p(4, 4) = p(3, 3) + p(4, 0) = 1 = 0 = 1

Sumujemy p(1, 4) do p (4, 4) = 1 + 2 + 1 + 1 = 5 sposobów

Sprawdzamy

3 + 1

2 + 2

2 + 1 + 1

1 +1 + 1 + 1

Jest to sposób identyczny z Rozmieszczeniem 2 (R₀₀₁), o którym napiszę wkrótce.

Pzykład 2

Jeżeli spojrzymy na ‘podstawę’ kolumny dla n = 7 w powyższej tabeli zobaczymy liczbę 15, co oznacza, że liczbę 7 można przedstawić jako sumę liczb naturalnych na 15 sposobów:

1,1,1,1,1,1,1
2,1,1,1,1,1
2,2,1,1,1
2,2,2,1
3,1,1,1,1
3,2,1,1
3,2,2
3,3,1
4,1,1,1
4,2,1
4,3
5,2
5,1,1
6,1
7

Kontynuacja tabeli:

n	11	12	13	14	15	16	17	18	19	20
p(n)	56	77	101	135	176	231	297	385	490	627

Wiadomo, że jeśli k = 2, to liczba partycji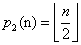

gdzie 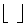oznacza zaokrąglenie do dołu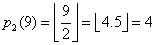

A oto liczba partycji dla następnych liczb:

n:
21: 792
22: 1002
23: 1255
24: 1575
25: 1958
26: 2436
27: 3010
28: 3718
29: 4565
30: 5604
31: 6842
32: 8349
33: 10143
34: 12310
35: 14883
36: 17977
37: 21637
38: 26015
39: 31185
40: 37338
41: 44583
42: 53174
43: 63261
44: 75175
45: 89134
46: 105558
47: 124754
48: 147273
49: 173525
50: 204226
51: 239943
52: 281589
53: 329931
54: 386155
55: 451276
56: 526823
57: 614154
58: 715220
59: 831820
60: 966467
61: 1121505
62: 1300156
63: 1505499
64: 1741630
65: 2012558
66: 2323520
67: 2679689
68: 3087735
69: 3554345
70: 4087968
71: 4697205
72: 5392783
73: 6185689
74: 7089500
75: 8118264
76: 9289091
77: 10619863
78: 12132164
79: 13848650
80: 15796476
81: 18004327
82: 20506255
83: 23338469
84: 26543660
85: 30167357
86: 34262962
87: 38887673
88: 44108109
89: 49995925
90: 56634173
91: 64112359
92: 72533807
93: 82010177
94: 92669720
95: 104651419
96: 118114304
97: 133230930
98: 150198136
99: 169229875
100: 190569292

Liczbę partycji dla dużych n można obliczyć używając wzoru:

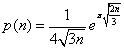
Kody

Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.

Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.