
Odwracanie macierzy (Java)
Macierz odwrotna
Macierz odwrotna A-1, to taka macierz, że po jej pomnożeniu przez A otrzymamy macierz jednostkową I:
A⋅A-1=A-1⋅A = I
Macierz odwrotna do macierzy A:
![]()
gdzie D jest transponowaną macierzą dopełnień algebraicznych odpowiadających elementów macierzy A.
Kroki przy odwracaniu macierzy:
- Pobieramy wszystkie podmacierze macierzy odwracanej
- Dla każdej podmacierzy obliczamy minor
- Obliczamy dopełnienie algebraiczne każdego minora
- Dopełnienia umieszczamy w macierzy
- Transformujemy macierz dopełnień
- Obliczamy wyznacznik macierzy odwracanej
- Mnożymy transformowaną macierz dopełnień przez odwrotność wyznacznika
Odwracanie macierzy
Załóżmy, że mamy do odwrócenia macierz:
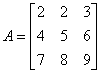
Pobieramy podmacierz ![]()
Obliczamy minor ![]()
Obliczamy dopełnienie algebraiczne minora = -3
Wstawiamy dopełnienie do macierzy dopełnień
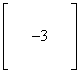
Powtarzamy operację dla wszystkich podmacierzy i otrzymujemy macierz dopełnień:
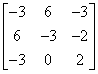
Transponujemy macierz dopełnień. Otrzymujemy macierz transponowaną:
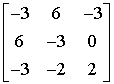
Obliczamy wyznacznik macierzy odwracanej.
Wyznacznik macierzy wyjściowej wynosi -3.
Mnożymy macierz transponowaną przez skalar (odwrotność wyznacznika macierzy wyjściowej)
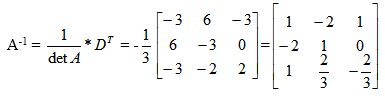
Sprawdzenie
A=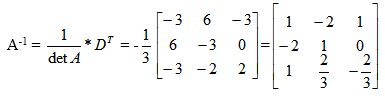
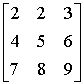
A-1=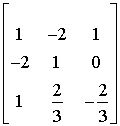
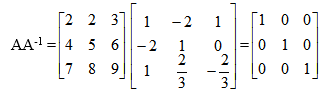
Ponieważ wynik mnożenia jest macierzą jednostkową, tzn. że macierz A-1 jest macierzą odwrotną do macierzy A.
Obliczenie w klasie Matrix034.
double[][] array = {{2, 2, 3}, {4, 5, 6}, {7, 8, 9}};
Matrix matrix = new Matrix(array);
matrix.printToConsole();
Util.print("");
Matrix matrixac = new Matrix(matrix.getRowCount(),
matrix.getColCount());
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
double ac = MatrixUtil.algComplement(matrix, i, j);
try {
matrixac.setCell(i, j, ac);
} catch (MatrixException e) {
e.printStackTrace();
}
}
}
Matrix matrix1 = MatrixUtil.transpose(matrixac);
double det = 0.0;
try {
det = matrix.det();
} catch (MatrixException e) {
e.printStackTrace();
}
Matrix matrixt = matrix1.mult2(1 / det);
matrixt.printToConsole();
Util.print("");
Matrix finalm = matrix.multiply2(matrixt);
finalm.printToConsole();
Po uruchomieniu klasy na konsoli zobaczymy:
2.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 0.5 -1.0 0.5 -1.0 0.5 0.0 0.5 0.3333333333333333 -0.3333333333333333 0.5 0.0 0.0 0.0 0.5 0.0 0.0 0.0 0.5
W klasie Matrix035 pokazano użycie metody inverse do odwracania macierzy
Eliminacja Gaussa – Jordana
Jeżeli będziemy wykonywali operacje elementarne tylko na wierszach, to każdą macierz nieosobliwą można sprowadzić do macierzy jednostkowej.
Jeżeli dla danej macierzy przyjmiemy macierz jednostkową o tym samym rozmiarze, to jeśli wykonamy operacje elementarne zarówno na macierzy wyjściowej, jak i na macierzy elementarnej, to macierz wyjściowa przekształci się w macierz jednostkową, a macierz jednostkowa – w macierz odwrotną.
Mamy macierz:
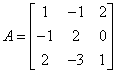
Wyznacznik macierzy ![]() , czyli macierz jest nieosobliwa, a jako taka ma macierz odwrotną.
, czyli macierz jest nieosobliwa, a jako taka ma macierz odwrotną.
Tworzymy macierz blokową [A|I] zawierającą macierz A oraz macierz jednostkową I.
Używając operacji elementarnych wyłącznie na wierszach sprowadzamy macierz blokową do postaci [I|B], gdzie macierz B jest macierzą odwrotną a-1.
1.0 -1.0 2.0 1.0 0.0 0.0 -1.0 2.0 0.0 0.0 1.0 0.0 2.0 -3.0 1.0 0.0 0.0 1.0 1.0 -1.0 2.0 1.0 0.0 0.0 0.0 1.0 2.0 1.0 1.0 0.0 2.0 -3.0 1.0 0.0 0.0 1.0 1.0 -1.0 2.0 1.0 0.0 0.0 0.0 1.0 2.0 1.0 1.0 0.0 0.0 -1.0 -3.0 -2.0 0.0 1.0 1.0 -1.0 2.0 1.0 0.0 0.0 0.0 1.0 2.0 1.0 1.0 0.0 0.0 0.0 -1.0 -1.0 1.0 1.0 1.0 -1.0 2.0 1.0 0.0 0.0 0.0 1.0 2.0 1.0 1.0 0.0 0.0 0.0 1.0 1.0 -1.0 -1.0 1.0 -1.0 2.0 1.0 0.0 0.0 0.0 1.0 0.0 -1.0 3.0 2.0 0.0 0.0 1.0 1.0 -1.0 -1.0 1.0 -1.0 0.0 -1.0 2.0 2.0 0.0 1.0 0.0 -1.0 3.0 2.0 0.0 0.0 1.0 1.0 -1.0 -1.0 1.0 0.0 0.0 -2.0 5.0 4.0 0.0 1.0 0.0 -1.0 3.0 2.0 0.0 0.0 1.0 1.0 -1.0 -1.0
Jeżeli pomnożymy macierz wejściową przez wyjściową otrzymamy macierz elementarną.
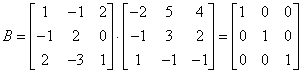
Operacja sprowadzania macierzy do postaci jednostkowej składa się z dwóch etapów:
- przekształcenie macierzy nieosobliwej w macierz górnotrójkątną – ten sposób opisano w podrozdziale poświęconym wyznacznikowi macierzy oraz przy omawianiu eliminacji Gaussa
- sprowadzenie macierzy górnotrójkątnej do macierzy jednostkowej
Zauważmy, że w tej metodzie nie martwimy się ani o znak wyznacznika w przypadku zamiany wierszy, ani o podzielenie wyznacznika przez skalar, którego użyliśmy do pomnożenia elementów wiersza.
Przykład w klasie Matrix077:
double[][] A = {{1, -1, 2}, {-1, 2, 0}, {2, -3, 1}};
Matrix m = new Matrix(A);
m.printToConsole();
Util.print("");
Matrix m1 = MatrixUtil.inverseGauss(m);
m1.printToConsole(2);
Util.print("");
Matrix m2 = MatrixUtil.multiply3(m, m1);
m2.printToConsole(1);
Util.print("");
Po uruchomieniu klasy na konsoli zobaczymy:
1.0 -1.0 2.0 -1.0 2.0 0.0 2.0 -3.0 1.0 -2.0 5.0 4.0 -1.0 3.0 2.0 1.0 -1.0 -1.0 1.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 1.0
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 023;

