Minor, dopełnienie algebraiczne i rząd macierzy (Java)

Minor, dopełnienie algebraiczne i rząd macierzy (Java)

Minor

Wyznacznik podmacierzy danej macierzy. Minor M_ij to wyznacznik podmacierzy, czyli macierzy, z której usunięto i-ty wiersz i j-tą kolumnę. Indeksy minorów i podmacierzy zaczynają się od 1 (ze względu na wykładniki potęg).

Macierz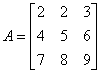

Podmacierz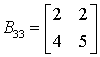

Minor M₃₃ tej podmacierzy to 2*5 – 2*4 = 2

Przykład w klasie Matrix031:

        double[][] array = {{2, 2, 3}, {4, 5, 6},
           {7, 8, 9}};
        Matrix matrix = new Matrix(array);
        matrix.printToConsole();
        Util.print("");
        double minor = MatrixUtil.minor(matrix, 2, 2);
        Util.print("minor(3,3): " + minor);

Po uruchomieniu klasy na konsoli zobaczymy:

2.0 2.0 3.0
4.0 5.0 6.0
7.0 8.0 9.0
minor(3,3): 2.0

Minor główny

To wyznacznik podmacierzy głównej.

Dopełnienie algebraiczne

Jest to iloczyn:

(-1)^i+j i minora M_ij

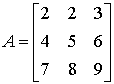
Podmacierz A22 =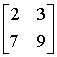

Minor M₂₂ = detA₂₂ = det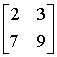 = 2*9 – 3*7 = -3

Dopełnienie algebraiczne elementu A₂₂ = (-1)²⁺² × -3 = 1 ×-3 = -3.

W macierzy dopełnień zaznaczamy:

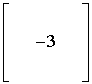
Przykład w klasie Matrix032:

       double[][] array = {{2, 2, 3}, {4, 5, 6},
               {7, 8, 9}};
        Matrix matrix = new Matrix(array);
        Matrix matrix1 = MatrixUtil.submatrix(matrix, 2, 2);
        matrix1.printToConsole();
        Util.print("");
        double minor = MatrixUtil.minor(matrix, 1, 1);
        Util.print("minor(2,2): " + minor);
        double algCompl = MatrixUtil.algComplement(matrix, 1, 1);
        Util.print("algCompl(2,2): " + algCompl);

Po uruchomieniu klasy na konsoli zobaczymy:

2.0 2.0
4.0 5.0
minor(2,2): -3.0
algCompl(2,2): -3.0

Jeżeli wykonamy wszystkie obliczenia uzyskamy macierz dopełnień:

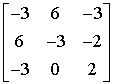
Przykład w klasie Matrix033:

       double[][] array = {{2, 2, 3}, {4, 5, 6},
              {7, 8, 9}};
        Matrix matrix = new Matrix(array);
        matrix.printToConsole();
        Util.print("");
        Matrix matrixac = new Matrix(matrix.getRowCount(),
                         matrix.getColCount());
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                double ac = MatrixUtil.algComplement(matrix, i, j);
                try {
                    matrixac.setCell(i, j, ac);
                } catch (MatrixException e) {
                    e.printStackTrace();
                }
            }
        }
        matrixac.printToConsole();
        double det = 0.0;
        try {
            det = matrix.det();
        } catch (MatrixException e) {
            e.printStackTrace();
        }
        Util.print("");
        Util.print("det: " + det);

Po uruchomieniu na konsoli zobaczymy:

2.0 2.0 3.0
4.0 5.0 6.0
7.0 8.0 9.0
-3.0 6.0 -3.0
6.0 -3.0 -2.0
-3.0 -0.0 2.0
det: -6.0

Rząd macierzy

Rząd macierzy A o wymiarach m×n to liczba r, która jest równa najwyższemu stopniowi nieosobliwej podmacierzy danej macierzy. r=0 dla macierzy zerowej. Rząd jest większy lub równy zero i mniejszy lub równy mniejszej z wartości (m,n)

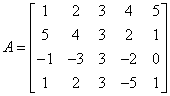
Macierz nie jest zerowa. Maksymalna wielkość podmacierzy, a więc i rząd macierzy

Badamy kolejno podmacierze zaczynając od największej:

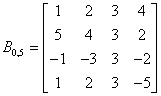
Obliczamy minor:

Ponieważ minor podmacierz B_{0, 5} jest nieosobliwa. Jej stopień r=4 jest rzędem macierzy A.

Przykład w klasie Matrix054:

       double[][] arr = {{1, 2, 3, 4}, {5, 4, 3, 2},
                {-1, -3, 3, -2}, {1, 2, 3, -5}};
        Matrix mat = new Matrix(arr);
        mat.printToConsole();
        double det = 0.0;
        try {
            det = MatrixUtil.det(mat);
        } catch (MatrixException e) {
            e.printStackTrace();
        }
        System.out.println(det);
        System.out.println("stopień:" + mat.size()[0]);

Po uruchomieniu klasy na konsoli zobaczymy:

1.0 2.0 3.0 4.0
5.0 4.0 3.0 2.0
-1.0 -3.0 3.0 -2.0
1.0 2.0 3.0 -5.0
432.0
stopień:4

Metoda eliminacji Gaussa

Inna definicja rzędu macierzy mówi, że jest to maksymalna liczba liniowo niezależnych wektorów tworzących kolumny (albo wiersze) danej macierzy. Zaletą tej definicji jest to, że jeżeli macierz sprowadzimy metodą eliminacji Gaussa do postaci schodkowej, to liczba niezerowych wierszy w tej macierzy jest rzędem macierzy.

Na stronie Wikipedii (hasło: 'Metoda eliminacji Gaussa’) znajduje się przykład, przy użyciu, którego sprawdzimy naszą metodę:

Macierz:

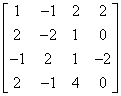
Macierz została sprowadzona do postaci schodkowej:

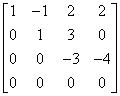
Ponieważ macierz ma trzy niezależne wiersze jej rząd wynosi 3.

Przykład w klasie Matrix070:

       double[][] array1 = {{1, -1, 2, 2}, {2, -2, 1, 0},
          {-1, 2, 1, -2}, {2, -1, 4, 0}};
        Matrix matrix1 = new Matrix(array1);
        matrix1.printToConsole();
        Util.print("");
        Matrix matrix2 = MatrixUtil.elimGauss(matrix1);
        matrix2.printToConsole();
        int rank = MatrixUtil.rankGauss(matrix1);
        Util.print(rank);

Po uruchomieniu klasy na konsoli zobaczymy:

1.0 -1.0 2.0 2.0
2.0 -2.0 1.0 0.0
-1.0 2.0 1.0 -2.0
2.0 -1.0 4.0 0.0
1.0 -1.0 2.0 2.0
0.0 1.0 1.5 -2.0
0.0 0.0 -3.0 -4.0
0.0 0.0 0.0 0.0
3

Jak widzimy wynik uzyskany ręcznie i wynik uzyskany przy użyciu naszego algorytmu jest identyczny.

Właściwości rzędu macierzy

1. Jeżeli macierz nie jest kwadratowa, to jej rząd jest mniejszy lub równy mniejszemu z wymiarów macierzy
2. Rząd macierzy równa się 0 wtedy i tylko wtedy, gdy macierz jest zerowa.
3. Macierz kwadratowa jest odwracalna wtedy i tylko wtedy, gdy jej rząd jest równy jej wymiarowi
4. Nierówność Sylwestra. Jeśli mamy dwie macierze kwadratowe A i B i obie są stopnia n, to wówczas
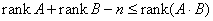
5. Transpozycja macierzy nie zmienia jej rzędu.
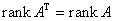
6. Operacje elementarne nie zmieniają rzędu

Ad. 1. Jeżeli macierz ma wymiar 4 × 3 to jej rząd jest równy 3 lub niższy.

Pliki do ściągnięcia

matrices022.zip

Moduł matrices – aktualny stan projektu = 022;

2019-12-01 08:46:37