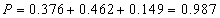Losowanie bez zwracania
Stosujemy wzór:
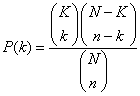
gdzie
k – liczba elementów wyróżnionych w wylosowanej próbie
n – liczebność wylosowanej próby
N – liczebność wszystkich elementów
K – całkowita liczba elementów wyróżnionych
Wzór stosuje się przy pobieraniu prób bez zwracania (losowanie bez zwracania).
Zadanie 1
Chomik syryjski zebrał na śniadanie 20 ziaren:
- 6 ziaren pszenicy
- 5 ziaren kukurydzy
- 3 ziarna żyta
- 4 ziarna owsa
- 2 ziarna jęczmienia
Gdy przyszedł czas na śniadanie – wsadził łapkę do kryjówki i wybrał porcję czterech ziaren do zjedzenia (losowanie bezzwrotne).
Jakie jest prawdopodobieństwo, że wśród wylosowanych ziaren znajduje się 1 ziarno kukurydzy?
k = 1 (interesująca nas liczba ziaren kukurydzy w porcji)
n = 4 (liczba ziaren w porcji)
N = 20 (ogólna liczba ziaren)
K = 5 (ogólna liczba ziaren kukurydzy)
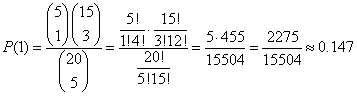
Zadanie 2
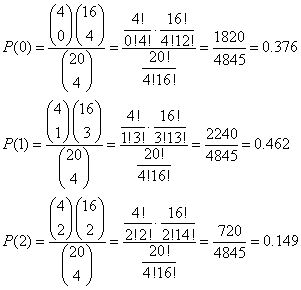
Pytanie 2. Jakie jest prawdopodobieństwo, że wśród wybranych ziaren (Przykład 1) znajdują się co najwyżej (nie więcej niż) dwa ziarna owsa.
Musimy zsumować 3 wyniki dla P(0), P(1), P(2).
k = 0, 1, 2 (interesująca nas liczba ziaren owsa w porcji)
n = 4 (liczba ziaren w porcji)
N = 20 (ogólna liczba ziaren)
K = 4 (ogólna liczba ziaren owsa)