Liczby Eulera I-go rodzaju (rzędu)
Liczby Eulera I-go rodzaju (rzędu)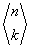 
wyrażają liczbę permutacji posiadających k wzniesień (wzgórz) wśród wszystkich permutacji zbioru n-elementowego.
Liczby Eulera możemy obliczyć z wzoru:
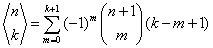
n>k
albo z rekurencyjnego wzoru:
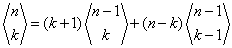
Wiemy, że:
, 
, 
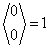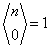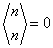
Przykład 1
Wzgórze to sytuacja, gdy przed daną liczbą (wzgórze) występuje liczba od niej mniejsza.
| n | k | Permutacje | |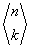
|---|---|---|---|
| 1 | 0 | {1} |  |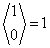
| 2 | 0 | {2,1} |  |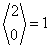
| 1 | {1,2} |  |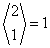
|
| 3 | 0 | {3,2,1} |  |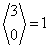
| 1 | {1,3,2}, {2,1,3}, {2,3,1}, {3,1,2} |  |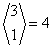
|
| 2 | {1,2,3} |  |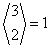
| k | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 1 | |||||||||||
| 1 | 1 | 0 | ||||||||||
| 2 | 1 | 1 | 0 | |||||||||
| 3 | 1 | 4 | 1 | 0 | ||||||||
| 4 | 1 | 11 | 11 | 1 | 0 | |||||||
| 5 | 1 | 26 | 66 | 26 | 1 | 0 | ||||||
| 6 | 1 | 57 | 302 | 302 | 57 | 1 | 0 | |||||
| 7 | 1 | 120 | 1191 | 2416 | 1191 | 120 | 1 | 0 | ||||
| 8 | 1 | 247 | 4293 | 15619 | 15619 | 4293 | 247 | 1 | 0 | |||
| 9 | 1 | 502 | 14608 | 88234 | 156190 | 88234 | 14608 | 502 | 1 | 0 | ||
| 10 | 1 | 1013 | 47840 | 455192 | 1310354 | 1310354 | 455192 | 47840 | 1013 | 1 | 0 | |
| 11 | 1 | 2036 | 152637 | 2203488 | 9738114 | 15724248 | 9738114 | 2203488 | 152637 | 2036 | 1 | 0 |
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.