
Liczby Bernoulliego
Liczby Bernoulliego to liczby pojawiające się jako współczynniki w rozwinięciu w szereg Taylora funkcji:
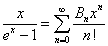
Mówiąc po ludzku, rozważamy wzory do obliczania sumy n kolejnych liczb (zaczynając od 0) podniesionych do potęgi m
Dla n = 5
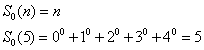
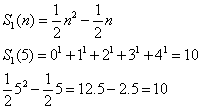
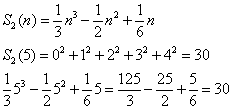
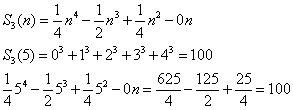
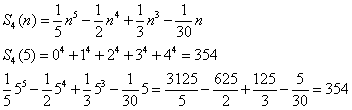
Uogólniając:
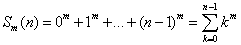
Liczby Bernoulliego są współczynnikami stojącymi przy liczbie n1 rozwinięcia:
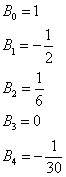
Uwagi
- Wszystkie liczby Bernoulliego, z wyjątkiem dla n = 0 są liczbami wymiernymi niecałkowitymi.
- Liczby Bernoulliego dla liczb nieparzystych n > 1 są równe 0.
Liczby Bernoulliego mają rozliczne zastosowania. Najlepiej zrobisz wyszukując w Internecie Bernoullli number wiki’, gdzie znajduje się największa liczba informacji o liczbach Bernoulliego.
Istnieje kilkadziesiąt wzorów pozwalających na obliczanie liczb Bernoulliego. Moim zdaniem
najlepszy i najprostszy jest wzór:
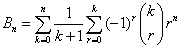
| n | Bn |
|---|---|
| 0 | 1 / 1 |
| 1 | -1 / 2 |
| 2 | 1 / 6 |
| 4 | -1 / 30 |
| 6 | 1 / 42 |
| 8 | -1 / 30 |
| 10 | 5 / 66 |
| 12 | -691 / 2730 |
| 14 | 7 / 6 |
| 16 | -3617 / 510 |
| 18 | 43867 / 798 |
| 20 | -174611 / 330 |
| 22 | 854513 / 138 |
| 24 | -236364091 / 2730 |
| 26 | 8553103 / 6 |
| 28 | -23749461029 / 870 |
| 30 | 8615841276005 / 14322 |
| 32 | -7709321041217 / 510 |
| 34 | 2577687858367 / 6 |
| 36 | -26315271553053477373 / 1919190 |
| 38 | 2929993913841559 / 6 |
| 40 | -261082718496449122051 / 13530 |
| 42 | 1520097643918070802691 / 1806 |
| 44 | -27833269579301024235023 / 690 |
| 46 | 596451111593912163277961 / 282 |
| 48 | -5609403368997817686249127547 / 46410 |
| 50 | 495057205241079648212477525 / 66 |
| 52 | -801165718135489957347924991853 / 1590 |
| 54 | 29149963634884862421418123812691 / 798 |
| 56 | -2479392929313226753685415739663229 / 870 |
| 58 | 84483613348880041862046775994036021 / 354 |
| 60 | -1215233140483755572040304994079820246041491 / 56786730 |
| 62 | 12300585434086858541953039857403386151 / 6 |
| 64 | -106783830147866529886385444979142647942017 / 510 |
| 66 | 1472600022126335654051619428551932342241899101 / 64722 |
| 68 | -78773130858718728141909149208474606244347001 / 30 |
| 70 | 1505381347333367003803076567377857208511438160235 / 4686 |
| 72 | -5827954961669944110438277244641067365282488301844260429 / 140100870 |
| 74 | 34152417289221168014330073731472635186688307783087 / 6 |
| 76 | -24655088825935372707687196040585199904365267828865801 / 30 |
| 78 | 414846365575400828295179035549542073492199375372400483487 / 3318 |
| 80 | -4603784299479457646935574969019046849794257872751288919656867 / 230010 |
| 82 | 1677014149185145836823154509786269900207736027570253414881613 / 498 |
| 84 | -2024576195935290360231131160111731009989917391198090877281083932477 / 3404310 |
| 86 | 660714619417678653573847847426261496277830686653388931761996983 / 6 |
| 88 | -1311426488674017507995511424019311843345750275572028644296919890574047 / 61410 |
| 90 | 1179057279021082799884123351249215083775254949669647116231545215727922535 / 272118 |
| 92 | -1295585948207537527989427828538576749659341483719435143023316326829946247 / 1410 |
| 94 | 1220813806579744469607301679413201203958508415202696621436215105284649447 / 6 |
| 96 | -211600449597266513097597728109824233673043954389060234150638733420050668349987259 / 4501770 |
| 98 | 67908260672905495624051117546403605607342195728504487509073961249992947058239 / 6 |
| 100 | -94598037819122125295227433069493721872702841533066936133385696204311395415197247711 / 33330 |
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

