Epicykloida (HTML5 canvas) - Blog Zielonego Smoka

Zielony Smok - logo witryny

Epicykloida

Jest to krzywa kreślona przez punkt M okręgu, który toczy się bez poślizgu po zewnętrznej stronie okręgu nieruchomego koła.

Epicykloida wyrażona jest równaniem parametrycznym:

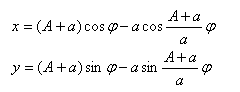
gdzie:

A– jest promieniem nieruchomego koła

a– jest promieniem ruchomego koła.

Kształt krzywej zależy od stosunku

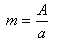Gdy:

m=1 powstaje krzywa zwana kardioidą
m jest liczbą całkowitą, epicykloida jest krzywą zamkniętą, składającą się ze skończonej liczby łuków
m jest ułamkiem, epicykloida składa się ze skończonej liczby krzyżujących się łuków. przy czym punkt bieżący wraca do punktu wyjściowego
m jest liczbą niewymierną, łuków jest nieskończenie wiele, a punkt M nie wraca do położenia wyjściowego.

Epitrochoida

Do równania epicykloidy, w drugim członie każdego równania można wprowadzić dodatkowy parametr λ.

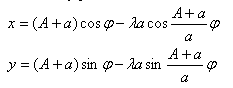
Jeżeli:

λ = 1 parametr ten jest równy 1 jak w powyższych wzorach otrzymujemy epicykloidę
λ > 0 to otrzymujemy tzw. epicykloidę wydłużoną
λ < 0 to otrzymujemy tzw. epicykloidę skróconą.

Wszystkie trzy epicykloidy noszą ogólną nazwę epitrochoida.

m=1 (A=60, a=60 ), λ=1

Listing

    var epicykloida = function(AA, aa, lambda, liczbaPunktow, strokeStyle) {
	ctx.save();
	ctx.beginPath();
	ctx.translate(w / 2, h / 2);
	ctx.strokeStyle = strokeStyle;
	var x1 = AA - (lambda - 1) * aa;
	var y1 = 0;
	var x2;
	var y2;
	for ( var i = 0; i < liczbaPunktow; i++) {
		var t = i * Math.PI / 360.0;
		x2 = (AA + aa) * Math.cos(t) - lambda * aa
				* Math.cos((AA + aa) * t / aa);
		y2 = (AA + aa) * Math.sin(t) - lambda * aa
				* Math.sin((AA + aa) * t / aa);
		ctx.moveTo(Math.floor(x1), Math.floor(y1));
		ctx.lineTo(Math.floor(x2), Math.floor(y2));
		x1 = x2;
		y1 = y2;
	}
	ctx.stroke();
	ctx.restore();
};
	var cv = document.getElementById("canvas");
	var ctx = cv.getContext("2d");
	var w = cv.width;
	var h = cv.height;
	epicykloida(60, 60, 1, 1000, "blue");