
Eliminacja Gaussa (Java)
Każdą macierz można przekształcić do postaci schodkowej używając operacji E,T oraz do postaci schodkowej zredukowanej przy pomocy operacji E, T, I.
Jeżeli podczas przekształcania macierzy nie używamy operacji T mówimy o eliminacji bez przestawiania.
Jeżeli podczas przekształcania macierzy używamy operacji T i wykonujemy operacje wyłącznie na wierszach – mówimy o eliminacji z przestawianiem częściowym.
Jeżeli używamy operacji T i wykonujemy operacje zarówno na wierszach jak i kolumnach – mówimy o eliminacji z przestawianiem pełnym.
Eliminacja bez przestawiania
Mamy macierz wyjściową:
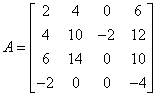
Zredukujmy macierz metodą eliminacji Gaussa bez przestawiania:
| Macierz | Operacja | Typ operacji |
|---|---|---|
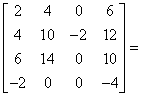 |
E | |
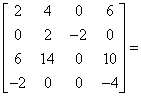 |
E | |
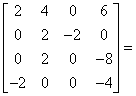 |
E | |
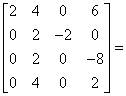 |
E | |
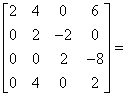 |
E | |
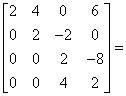 |
E | |
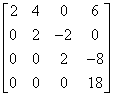 |
– | – |
Do wykonania powyższego moglibyśmy użyć metody MatrixUtil.naiveGauss. Przykład w klasie Matrix083:
double[][] A = {{2, 4, 0, 6}, {4, 10, -2, 12},
{6, 14, 0, 10}, {-2, 0, 0, -4}};
Matrix m = new Matrix(A);
m.printToConsole();
Util.print("");
Matrix m1 = MatrixUtil.naiveGauss(m);
m1.printToConsole();
Util.print("");
Po uruchomieniu klasy na konsoli zobaczymy:
2.0 4.0 0.0 6.0 4.0 10.0 -2.0 12.0 6.0 14.0 0.0 10.0 -2.0 0.0 0.0 -4.0 2.0 4.0 0.0 6.0 0.0 2.0 -2.0 0.0 0.0 0.0 2.0 -8.0 0.0 0.0 0.0 18.0
Jak widzimy uzyskaliśmy identyczną macierz jak przy metodzie 'ręcznej’.
Ostrzeżenie 1
Eliminacja Gaussa jest prosta. Kłopoty zaczynają się w momencie, gdy któryś z elementów stojących na przekątnej jest lub stanie się zerem w trakcie przekształcenia. Wystąpi dzielenie przez zero i komputer wyrzuci wyjątek. Na ogół konieczne jest więc przestawianie wierszy.
Eliminacja z przestawianiem częściowym
Jeżeli zachodzi potrzeba wiersze należy przestawić. Np . jeśli element jest zerowy, a macierz jest nieosobliwa, to w pierwszej kolumnie z pewnością istnieje element niezerowy. Musimy go znaleźć i zamienić wiersze. Przestawienie możemy wykonać przestawiając wiersze w obiekcie Matrix albo przestawiając wiersze jedynie w algorytmie.
Przestawianie wierszy macierzy
Do przestawienia wierszy macierzy możemy użyć metody elimGauss w klasie MatrixUtil.
Operacje elementarne wykonujemy przy pomocy wyspecjalizowanych metod, które dokonują operacji elementarnych bez tworzenia macierzy przekształceń: operT, operE, operI,
getCell, countStartZeroes – wszystkie w klasie MatrixUtil.
Przykład w klasie Matrix069:
double[][] array = {{2, 4, 0, 6}, {4, 10, -2, 12},
{6, 14, 0, 10}, {-2, 0, 0, -4}};
Matrix matrix = new Matrix(array);
matrix.printToConsole();
Util.print("");
Matrix matrix1 = MatrixUtil.elimGauss(matrix);
matrix1.printToConsole();
Wykonaliśmy eliminację dla tej samej macierzy aby sprawdzić algorytm, ale możesz być pewny
Czytelniku/Czytelniczko, że jeśli niepotrzebne zera będą w macierzy, to algorytm sobie z nimi poradzi.
Po uruchomieniu kodu na konsoli zobaczymy:
2.0 4.0 0.0 6.0 4.0 10.0 -2.0 12.0 6.0 14.0 0.0 10.0 -2.0 0.0 0.0 -4.0 2.0 4.0 0.0 6.0 0.0 2.0 -2.0 0.0 0.0 0.0 2.0 -8.0 0.0 0.0 0.0 18.0
Możemy zauważyć, że macierz obliczona 'ręcznie’ jest identyczna jak obliczona przy użyciu algorytmu.
Przestawienie wierszy w algorytmie
Zamiast zamieniać fizycznie wiersze w macierzy wystarczy stworzyć tablicę przestawną, nazywaną też tablicą przestawień albo tablicą permutacji, która określi kolejność wierszy przy wykonywaniu eliminacji.
Wiersze oznaczone są numerami 1,2,3. Ponieważ pracujemy na tablicach oznaczymy je 0,1,2. Te wiersze mogą być dowolną permutacją tego zbioru, czyli możemy np. wykonać działania w kolejności {2,1,0} lub jakiejkolwiek innej możliwej. Wybór właściwej permutacji wierszy omówimy oddzielnie.
Możemy użyć metody permutGauss w klasie MatrixUtil:
public static Matrix permutGauss(Matrix matrix, int[] perm) {
Matrix mat = null;
try {
mat = matrix.clone();
} catch (CloneNotSupportedException e) {
e.printStackTrace();
}
int n = mat.getRowCount();
for (int k = 0; k <= n - 1; k++) {
for (int i = k + 1; i < n; i++) {
double z = getCell(mat, perm[i], k) / getCell(mat,
perm[k], k);
setCell(mat, perm[i], k, 0);
for (int j = k + 1; j < n; j++) {
setCell(mat, perm[i], j, getCell(mat, perm[i], j)
- z * getCell(mat, perm[k], j));
}
}
}
return mat;
}
Przykład w klasie Matrix084.
Wykonujemy operacje w kolejności {0,1,2}:
double[][] A = {{2, 3, -6}, {1, -6, 8},
{3, -2, 1}};
Matrix m = new Matrix(A);
m.printToConsole();
Util.print("");
Matrix m1 = MatrixUtil.naiveGauss(m);
m1.printToConsole();
Util.print("");
int[] tabl = {0, 1, 2};
Matrix m2 = MatrixUtil.permutGauss(m, tabl);
m2.printToConsole();
Util.print("");
Po uruchomieniu klasy na konsoli zobaczymy:
Macierz: 2.0 3.0 -6.0 1.0 -6.0 8.0 3.0 -2.0 1.0 naiveGauss: 2.0 3.0 -6.0 0.0 -7.5 11.0 0.0 0.0 0.4666666666666668 permutGauss 2.0 3.0 -6.0 0.0 -7.5 11.0 0.0 0.0 0.4666666666666668
Ostrzeżenie 2
Problemy z algorytmem Gaussa będziemy również mieli wtedy, gdy różnica między największymi, a najmniejszymi elementami w macierzy jest bardzo dużo. Problemów można uniknąć zmieniając w określony sposób kolejność wierszy w tabeli przestawnej i kolejność wykonywania eliminacji czyli wykonując skalowanie, nazywane dokładniej skalowalnym wyborem wierszy.
Zastosowania
Metodę eliminacji Gaussa stosuje się do:
1. obliczania wyznacznika macierzy
2. obliczania rzędu macierzy
3. obliczania macierzy odwrotnej
4. rozwiązywania układów równań liniowych
Każde z wypunktowanych zagadnień zostało omówione w oddzielnym podrozdziale w rozdziałach omawiających powyższe zagadnienia.
Zastosowania
Metodę eliminacji Gaussa stosuje się do:
- obliczania wyznacznika macierzy
- obliczania rzędu macierzy
- obliczania macierzy odwrotnej
- rozwiązywania układów równań liniowych
Każde z wypunktowanych zagadnień zostało omówione w oddzielnym podrozdziale w rozdziałach omawiających powyższe zagadnienia.
Pliki do ściągnięcia
matrices021.zip
Moduł matrices – aktualny stan projektu = 021;

