
Definicja i rodzaje ułamków
Definicja ułamka zwykłego
Ułamek zwykły to liczba zapisana w postaci: licznik, kreska ułamkowa, mianownik:

Licznik jest liczbą całkowitą (licznik ∈ ℤ), a więc może być liczbą dodatnią, ujemną albo zerem.
Jeżeli licznik jest liczbą ujemną, znak liczby zapisujemy przed kreską ułamkową:
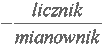
Mianownik jest liczbą naturalną (mianownik ∈ ℕ), a więc nie może być zerem.
![]()
Mianownik ułamka określa całość. Licznik określa część tej całości.
Kreska ułamkowa
Kreska ułamkowa może być pozioma (jak wyżej) albo ukośna:
![]()
Kreska ułamkowa zarówno pozioma jak i ukośna oznaczają dzielenie licznika przez mianownik, czyli kreska ułamkowa jest równoważna znakowi dzielenia.
Znaki, które mogą mieć zastosowanie jako kreska ułamkowa ukośna to:
1) 3/4 ukośnik prawy,
2) 3⁄4 ukośnik ułamkowy
3) 3∕4 ukośnik dzielenia
Ułamki właściwe
Mamy ułamek zwykły:
![]()
Jeżeli |c|< n (bezwzględna wartość licznika jest mniejsza od mianownika) ułamek jest nazywany ułamkiem właściwym.
Przykłady:
![]()
![]()
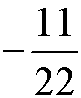
Ułamki niewłaściwe
Mamy ułamek zwykły:
![]()
Jeżeli |c| ≥ n (bezwzględna wartość licznika jest większa od mianownika albo równa mianownikowi) ułamek jest nazywany ułamkiem niewłaściwym.
Przykłady:
![]()
![]()
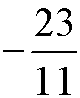
![]()
Ułamki mieszane
Ułamek mieszany (liczba mieszana) to ułamek niewłaściwy zapisany w postaci ułamka właściwego z dodaniem poprzedzającej go liczby całkowitej:
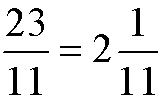
Ułamki nieskracalne
Jeżeli |c| (bezwzględna wartość licznika) i n są względnie pierwsze, ułamek nazywamy ułamkiem nieskracalnym.
Przykłady:
![]()
![]()
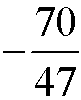
Ułamki skracalne
Mamy ułamek zwykły:
![]()
Jeżeli |c| (bezwzględna wartość licznika) i n nie są względnie pierwsze, ułamek nazywamy ułamkiem skracalnym.
Przykłady:
![]()
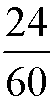
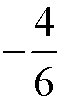
Ułamki proste
Ułamek prosty to ułamek właściwy o postaci:
![]()
gdzie n jest liczbą naturalną.
Przykłady:
![]()
![]()
Każdy ułamek właściwy można zapisać jako sumę ułamków prostych.
Ułamki dziesiętne
Ułamek dziesiętny to ułamek zwykły o postaci:
![]()
(mianownik ułamka dziesiętnego jest potęgą liczby 10).
Ułamki dziesiętne na ogół zapisuje się w postaci rozwinięć dziesiętnych.
Przykłady:
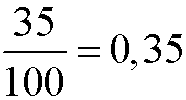
Ułamki łańcuchowe
Ułamek łańcuchowy (ułamek ciągły) to wyrażenie postaci:
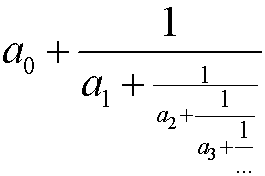
Ułamki łańcuchowe nie są przedmiotem naszego zainteresowania i nie będą dokładniej omawiane.

