Filotaksja (ulistnienie) i złoty kąt
Opisuje sposób rozmieszczenia liści na łodydze.
Liście na łodydze
Z węzła na łodydze wyrasta jeden lub więcej liści. Na rysunkach liście oznaczone są zielonymi kołami.
Na rysunkach kolejne węzły oznaczone są jako coraz mniejsze okręgi.
Kąt d zaznaczany na rysunkach jest kątem dywergencji, czyli kątem między kierunkami liści na kolejnych węzłach.
Ulistnienie skrętoległe
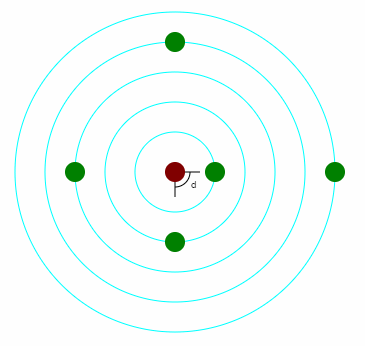
Gdy z węzła wyrasta jeden liść, a linia łącząca nasady liści obiega łodygę spiralnie, wówczas mówimy o ustawieniu skrętoległym.
Ulistnienie naprzemianległe
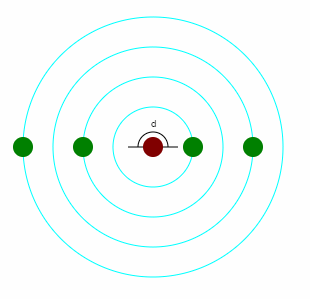
Gdy z węzła wyrasta jeden liść, a są dwie linie łączące nasady liści, kolejne liście wyrastają z różnych węzłów (co drugi w rzędzie), wówczas mówimy o ustawieniu naprzemianległym.
Ulistnienie okółkowe
Gdy z węzła wyrasta więcej niż jeden liść mówimy o ulistnieniu okółkowym.
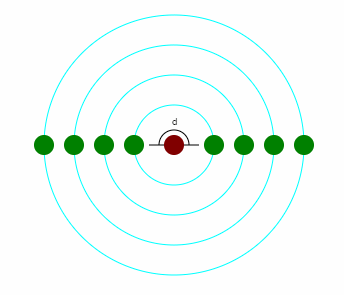
Gdy w ulistnieniu okółkowym z węzła wyrastają dwa liście to albo występuje jeden rząd i kolejne pary liści występują jedna nad drugą (są w jednej płaszczyźnie) i mówimy o ulistnieniu naprzeciwległym albo występują dwa rzędy (kolejna para liści liści jest przekręcona o 90°, i są dwie płaszczyzny) i mówimy o ulistnieniu nakrzyżległym.
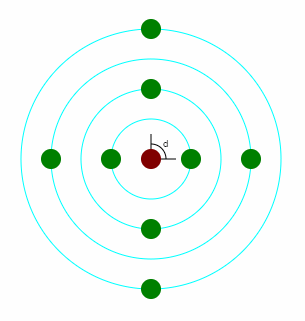
Oczywiście przy ulistnieniu okółkowym z każdego węzła może wychodzić więcej niż dwa liście.
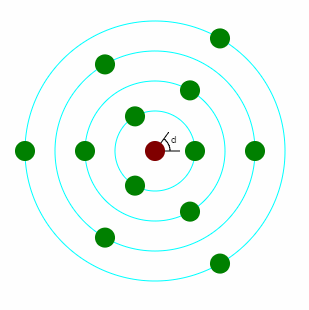
Ulistnienie spiralne
Kąt dywergencji
W każdym przypadku, gdy kąt d jest kątem wyrażonym liczbą całkowitą, albo dowolnym kątem wyrażonym liczbą wymierną, która da się przedstawić w postaci ułamka zwykłego lub okresowego – otrzymujemy radialny (promienisty) układ liści, gdyż wcześniej czy później następny liść wyrasta dokładnie ponad już istniejącym liściem.
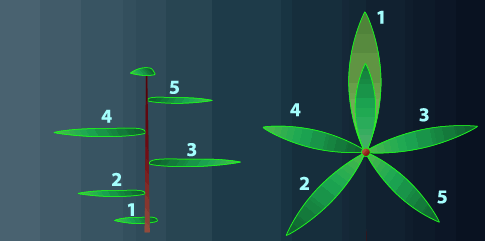
Szósty liść wyrasta dokładnie nad pierwszym (144° x 5 = 720°; 720° % 360° = 0; 720° / 360° = 2) po wykonaniu 2 'obiegów’ wokół rośliny.
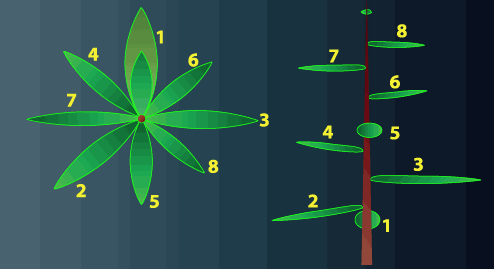
9 liść wyrasta dokładnie nad pierwszym po wykonaniu 3 'obiegów’ wokół rośliny (135° x 8 = 1080°; 1080° % 360° = 0; 1080° / 360° = 3).
Dopiero, gdy kąt d jest liczbą niewymierną – otrzymujemy filotaksję spiralną.
Złoty kąt
Kąt pełny 360° również podlega złotemu podziałowi, gdzie kąt pełny ma się tak do większej części, jak większa część do mniejszej.
![]()
Po rozwiązaniu otrzymujemy:
![]()
Kąt dywergencji d
![]()
jest złotym kątem. Jest liczbą niewymierną, więc nie da się przedstawić w postaci ułamka zwykłego.
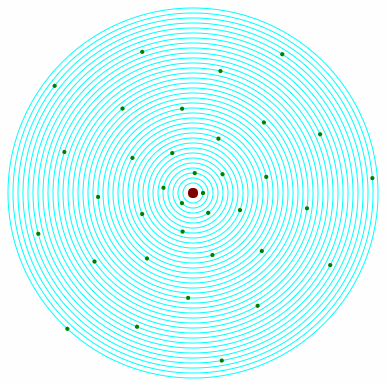
Gdybyśmy od stożka wzrostu poprowadzili linię do każdego liścia zauważylibyśmy, że żadne dwa liście nie leżą na jednej prostej, mimo, że roślina na już 35 liści.
Jedynie kąty niewymierne zapewniają pełne wykorzystanie przestrzeni.
Jedynie kąty niewymierne zapewniają powstanie układu spiralnego.

Układy spiralne spotykamy w wielu roślinach. Szczególnie znanym przykładem jest
słonecznik.

