
Krzywe Lissajous
Krzywa parametryczna zakreślana przez punkt wykonujący niezależne ruchy harmoniczne w dwóch płaszczyznach wzajemnie prostopadłych. Krzywe są opisane równaniem parametrycznym:
x = A*sin(a*t+ φ)
y = B*sin(b*t)
| a/b | A i B | φ | Kształt |
|---|---|---|---|
| 1 | dowolne | dowolne | elipsa |
| 1 | A = B | Math.PI/2 | okrąg |
| 1 | A = B | 0 | prosta |
| 2 | dowolne | Math.PI/2 | parabola |
| wymierne | Math.PI/2 | krzywa zamknięta | |
| niewymierne | Math.PI/2 | krzywa się nie zamyka i wypełnia całą przestrzeń |
A oto przykłady:
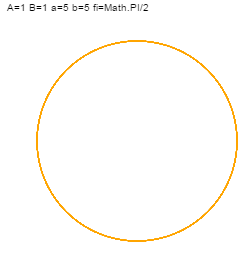


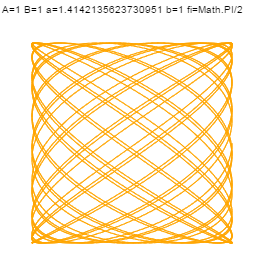
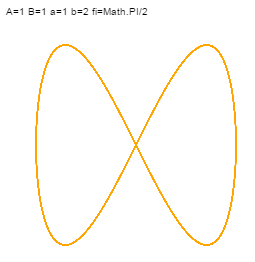
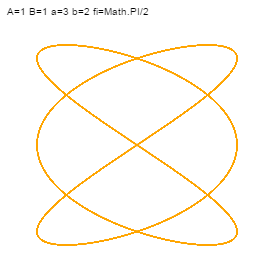
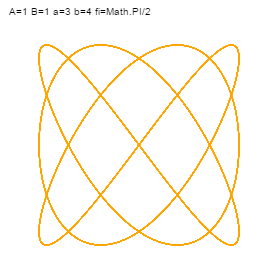
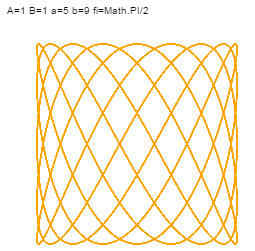
I jeszcze jeden przykad:
Listing
var lissajous = function(A, B, a, b, fi, liczbaPunktow, strokeStyle) {
ctx.save();
ctx.beginPath();
ctx.strokeStyle = strokeStyle;
ctx.translate(w / 2, h / 2);
var x2;
var y2;
for ( var i = 0; i < liczbaPunktow; i++) {
var t = i * Math.PI / 360;
x2 = A * Math.sin(a * t + fi);
y2 = B * Math.sin(b * t);
ctx.lineTo(x2, y2);
}
ctx.stroke();
ctx.restore();
};
var cv = document.getElementById("canvas");
var ctx = cv.getContext("2d");
var w = cv.width;
var h = cv.height;
var A=1;
var B=1
var a=9;
var b=8;
var fi = Math.PI/2.0;
lissajous(A*100, B*100, a, b, fi, 12000, "orange");
ctx.fillText("A="+A + " B="+B + " a="+a+" b="+b + " fi=Math.PI/2",20,20);

