Liczby i ciąg Fibonacciego
Ciąg Fibonacciego
Jest to ciąg liczb naturalnych określonych rekurencyjnie:
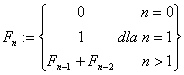
czyli:
F0 = 0 (niektórzy matematycy nie zaliczają 0 do wyrazów ciągu)
F1 = 1
F2 = 0 + 1 = 1
F3 = 1 + 1 = 2
F4 = 2 + 1 = 3
F5 = 3+ 2 = 5
F6 = 5 + 3 = 8
F7 = 8 + 5 = 13
A oto pierwsze 92 wyrazy ciągu.
Granica
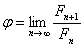
Stosunek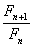 
przy n dążącym do nieskończoności dąży do liczby Φ (która jest granicą ciągu), czyli im dalsze wyrazy ciągu porównujemy, tym stosunek ten jest lepszym przybliżeniem liczby Φ.
Wzór Bineta
Jeżeli chcemy obliczyć n-ty wyraz ciągu możemy skorzystać z wzoru Bineta:
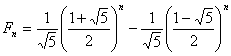
Ponieważ drugi człon równania szybko zbiega do 0 można, szczególnie przy dalszych wyrazach ciągu, używać wzoru:
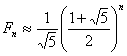np. 
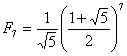= 12.98 ≈ 13
Inna postać tego wzoru:
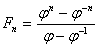
Dwusetny wyraz ciągu obliczony w ten sposób:
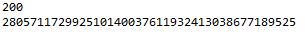
10-tysięczny wyraz ciągu F10000=
3364476487643178326662161200510754331030214846068006390656476997468008144216666 2368155595513633734025582065332680836159373734790483865268263040892463056431887 3545443695598274916066020998841839338646527313000888302692356736131351175792974 3785441375213052050434770160226475831890652789085515436615958298727968298751063 1200575428783453215515103870818298969791613127856265033195487140214287532698187 9620469360978799003509623022910263681314931952756302278376284415403605844025721 1433496118002309120828704608892396232883546150577658327125254609359112820392528 5393434620904245248929403901706233888991085841065183173360437470737908552631764 3257339937128719375877468974799263058370657428301616374089691784263786242128352 5811282051637029808933209990570792006436742620238978311147005407499845925036063 3560933883831923386783056136435351892133279732908133732642652633989763922723407 8829281779535805709936910491754708089318410561463223382174656373212482263830921 0329770164805472624384237486241145309381220656491403275108664339451751216152654 5361333111314042436854805106765843493523836959653428071768775328348234345557366 7197313927462736291082106792807847180353291311767789246590899386354593278945237 7767440619224033763867400402133034329749690202832814593341882681768389307200363 4795623117103101291953169794607632737589253530772552375943788434504067715555779 0564504430166401194625809722167297586150269684431469520346149322911059706762432 6851599283470989128470674086200858713501626031207190317208609408129832158107728 2076353186624611278245537208532365305775956430072517744315051539600905168603220 3491632226408852488524331580515348496224348482993809050704834824493274537326245 6775587908918719080366205800959474315005240253270974699531877072437682590741993 9632265984147498193609285223945039707165443156421328157688908058783183404917434 5562705202235648464951961124602683139709750693826487066132645076650746115126775 2274862159864253071129844118262266105716351506926002986170494542504749137811515 4139941550671256271197133252763631939606902895650288268608362241082050562430701 794976171121233066073310059947366875
Liczba cyfr w powyższej liczbie:
[217, 199, 228, 254, 194, 202, 217, 198, 197, 184, 2090]
Kolejne liczby oznaczają częstość występowania 0, 1, 2,…9. Ostatnia liczba określa sumę poprzedzających ją liczb.
Najważniejsze właściwości
Właściwość 1
Wyrazy ciągu Fibonacciego można wyrazić za pomocą symbolu Newtona jako:
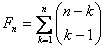
gdzie:
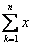oznacza sumę x-ów od k=1 do k=n,
co znaczy, że np.
= 
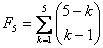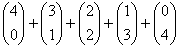=1+3+1+0+0=5
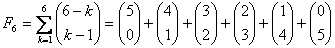= 1 + 4 + 3 + 0 + 0 + 0 = 8
Jeżeli zaznaczymy kolejne wyrazy ciągu:
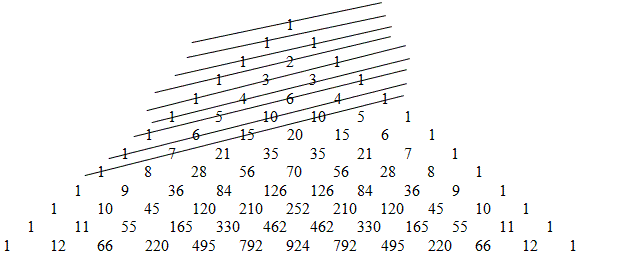
to zobaczymy, że sumy wyrazów leżących na kolejnych prostych równoległych są kolejnymi wyrazami ciągu Fibonacciego.
Przykład
F3 = 2, F6=8, F9=34, etc.
Właściwość 2
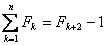
co znaczy, że np suma wyrazów ciągu od pierwszego do k-tego równa się wyrazowi k+2 od którego odjęto 1
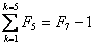
Suma wyrazów od k = 1 do k = 5 wynosi
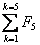= 0 + 1 + 1 + 2 + 3 + 5 = 12
F7 = 13
czyli,
12 = 13 – 1
Przykład
F3=3, F7=21, F11=89, etc.
Właściwość 3
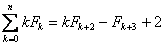
Jeżeli k = 5 to:
F0 = 0, k = 0
F1 = 1, k = 1
F2 = 1, k = 2
F3 = 2, k = 3
F4 = 3, k = 4
F5 = 5, k = 5
mnożymy kolejno wyrazy ciągu przez k:
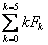= 0*0 + 1*1 + 1*2 + 2*3 + 3*4 + 5*5 = 0 + 1 + 2 + 6 + 12 + 25 = 46
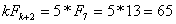
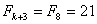
czyli 46 = 65 – 21 + 2
Przykład
n = 8, k = 4, to ponieważ 8 dzieli się przez 4 to F8 dzieli się przez F4
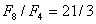
Właściwość 4
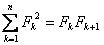
czyli suma kwadratów wyrazów ciągu od k = 1 do k jest równa iloczynowi k-tego wyrazu ciągu przez wyraz k + 1.
Jeżeli k = 6, to suma kwadratów równa się:
1*1+1*1+2*2+3*3+5*5+8*8=104
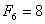
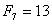
104 = 8*13
Największy wspólny dzielnik (nwd)
Liczba d jest nwd liczb a i b jeśli spełnione są dwa warunki:
- a dzieli się przez d i b dzieli się przez d
- jeżeli a dzieli się przez c i b dzieli się przez c, to i d dzieli się przez c
Przykład
F18 = 2584, czyli m = 18
F15 = 610, czyli n = 15
nwd(m,n) = nwd(18, 15) = 3
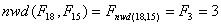
Właściwość 5
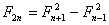
Jeżeli n = 4 to
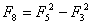
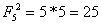
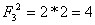
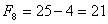
Właściwość 6
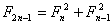
Jeżeli n =4, to
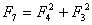
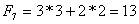
Właściwość 7
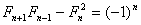
Jeżeli n = 5 to
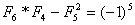
8*3 – 25 = 24-25=-1
Właściwość 8
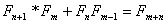
Jeżeli np. n = 5, m = 4 to
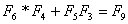
8*3 + 5*2 = 24 + 10 = 34 =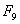
Właściwość 9
Jedyne liczby w ciągu, które są kwadratami liczb całkowitych to 1 i 144.
Właściwość 10
Każda liczba naturalna (a więc również liczba Fibonacciego) ma wielokrotność, która jest liczbą Fibonacciego, np. 5 ma wielokrotność 55, 4 ma wielokrotność 144, etc.
Właściwość 11
Istnieje nieskończenie wiele liczb n dla których zachodzi podzielność Fn przez n. Szczególnie można wykazać, że jeśli n jest liczbą naturalną, to
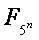jest podzielne przez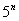 
Jeżeli n = 2 to
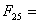75025
jest podzielne przez 25
Właściwość 12
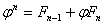
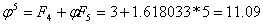
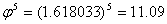
Właściwość 13
- Co trzecia liczba Fibonacciego jest podzielna przez 2
- Co czwarta liczba jest podzielna przez 3
- Co można uogólnić: Jeśli n dzieli się przez k to Fn dzieli się przez Fk
- Największy wspólny dzielnik dwóch liczb Fibonacciego jest liczbą Fibonacciego, której numer jest równy największemu wspólnemu dzielnikowi numerów tych liczb:
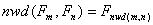
Właściwość 14
Każda liczba jest sumą dwóch lub więcej liczb Fibonacciego. Np. liczba 999999 jest sumą 7 liczb Fibonacciego:
2 + 5 + 13 + 34 + 144 + 46368 + 121393 + 832040
Inne właściwości
W literaturze można spotkać setki właściwości.
Ciekawostki, występowanie i zastosowania
F10000 jest numerologiczną szóstką.
Kwadraty Fibonacciego
Jest to ciąg kwadratów, których długości boków są kolejnymi liczbami Fibonacciego.
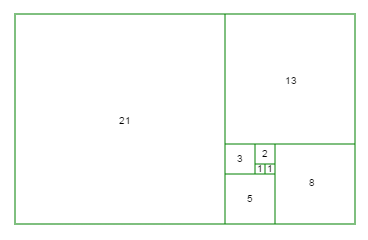
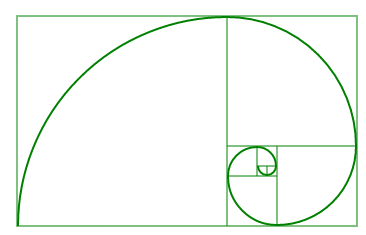
Spirala Fibonacciego
Jeżeli w kwadraty Fibonacciego wpiszemy ćwiartki łuku uzyskamy spiralę Fibonacciego bardzo podobną do złotej spirali.
Ciąg Fibonacciego w systemie dwójkowym
Jeśli kolejne wyrazy zapiszemy w systemie dwójkowym, jeden pod drugim, z wyrównaniem do prawej strony, po zastąpieniu każdej jedynki kolorowym kwadracikiem o boku 1, to otrzymamy strukturę przypominającą fraktal.
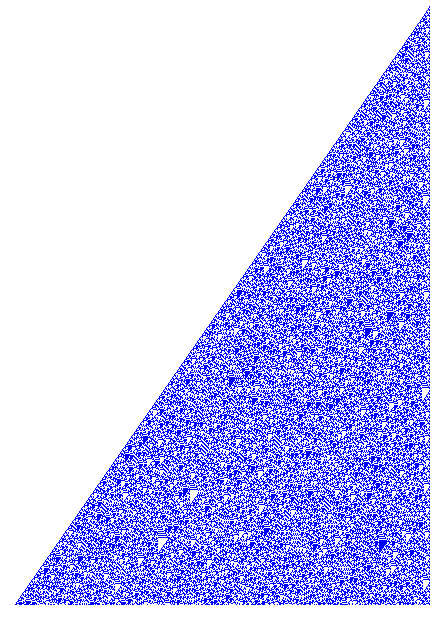
Liczby Rahaba
Szczegółowe informacje znajdziesz tutaj
Wśród błonkówek
Samce pszczoły (trutnie) powstają bez udziału ojca, mają tylko matkę (królową).
Królowe mają ojca (trutnia) i matkę (królową).
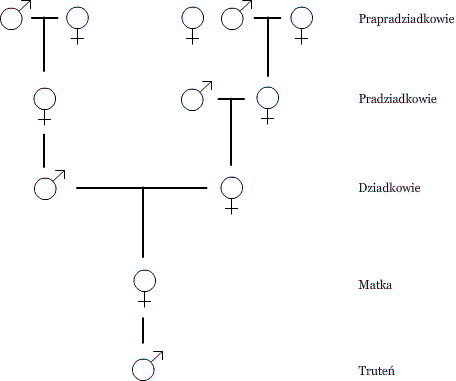
| Pokolenie (n) | Samica | Truteń | Razem |
|---|---|---|---|
| 0 | 1 | ||
| 1 | 1 | 1 | |
| 2 | 1 | 1 | 2 |
| 3 | 2 | 1 | 3 |
| 4 | 3 | 2 | 5 |
| Ogółem | n-1 | n-2 | (n-1)+(n-2) |
Jak widzimy kolejne liczby przodków są liczbami Fibonacciego.
Rozmnażanie królików
Zadanie Fibonacciego
Ile par królików będziesz miał po roku jeśli:
- Zaczynamy od jednej pary królików.
- Każda nowa para staje się płodna po 2 miesiącach.
- Każda para rodzi jedną nową parę co miesiąc.
- Króliki w tym czasie nie umierają.
Rozwiązanie
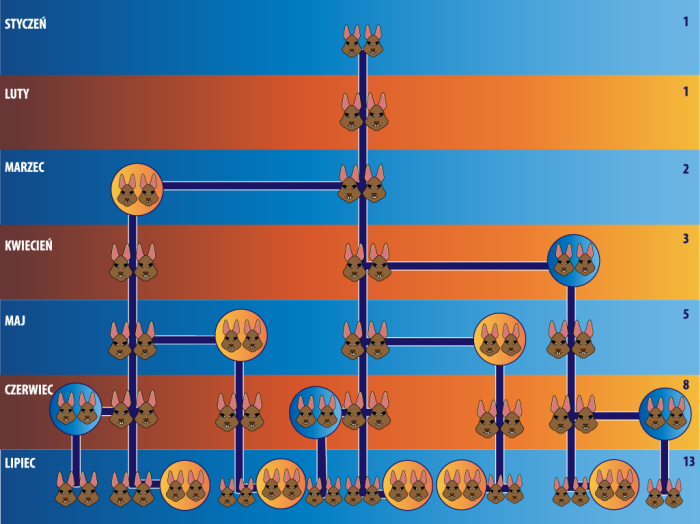
Jak widzimy liczba par to kolejne liczby ciągu Fibonacciego. tzn., że w grudniu będzie ich 144, a w styczniu 233.
Filotaksja i złoty kąt
Pędy boczne na pędzie głównym
Zadanie
Drzewo co roku wypuszcza nowe pędy, a każda nowa gałąź wypuszcza nowy pęd dopiero po dwóch latach. Ile gałęzi będzie miało drzewo po 6 latach?
Rozwiązanie
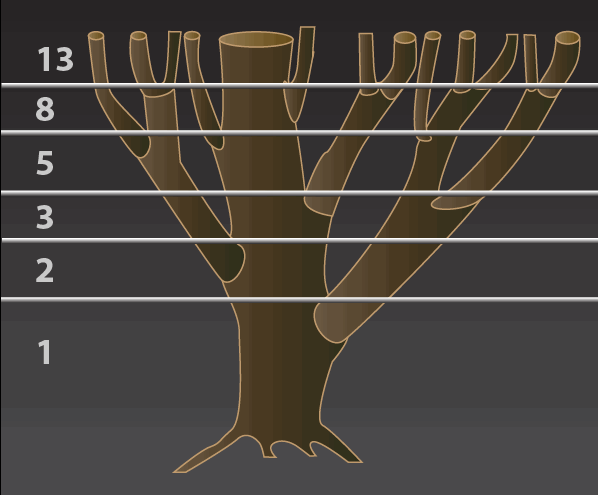
Więcej biologii
Odległość między spiralami DNA i skok tych spiral jest zgodna z liczbą φ.
Kształty roślin i ich części
W owocu ananasa 8 linii spiralnych biegnie w jedną stronę, a 5 albo 13 w drugą stronę.
Na tarczy słonecznika krzyżuje się 21 i 34 albo 55, a czasami 89 spiral (lub nawet więcej).
Różyczki kalafiora ułożone są spiralnie.
Łuski szyszek wielu gatunków są ułożone spiralnie.
Liczba płatków w kwiatach u wielu gatunków jest liczbą Fibonacciego (jest to cecha gatunkowa). Spotyka się liczby: 3, 5, 8, 13, 21, 34, 55, 89. Oczywiście znaczna liczba gatunków ma liczbę płatków, która nie jest liczbą Fibonacciego.
Kształty zwierząt i ich części
Muszle ślimaków tworzą skręty zgodne ze spiralą Fibonacciego.
Proporcje ciała niektórych bezkręgowców zbliżają się do liczby φ.
Muzyka
Utwory muzyczne
Liczby i ciąg Fibonacciego spotykane są np. w muzyce i są widoczne w rytmie i harmonii oraz długości dźwięków w niektórych utworach muzycznych. Jeżeli jesteś zainteresowany tym tematem, to znajdziesz sporo ogólnikowych informacji w Internecie. Dokładniejsze wymagały by większej wiedzy muzycznej i dostępu do nut utworów w celu szczegółowej analizy.
Proporcje skrzypiec
Literatura
Np. w powieści D. Browna „Kod Leonarda da Vinci” ciąg Fibonacciego ma istotne znaczenie dla przebiegu akcji.
Liczby Fibonacciego w kulturze masowej
Ekonomia
W przyrodzie istnieją prawa natury (ustanowione przez Boga lub nie), np. dobór naturalny, które wymuszają efektywność energetyczną, co często skutkuje wykorzystaniem układów opisywanych przez liczbę φ i wyrazy ciągu Fibonacciego. W ekonomii nie ma żadnego prawa (ani czynnika), które nakazywało by np. zmianom kursów akcji na giełdzie przebiegać w jakiś mniej czy bardziej efektywny sposób lub zgodny z jakimś wzorem czy układem. Dlatego wszelkie zbieżności trendów z ciągiem Fibonacciego są przypadkowe i krótkotrwałe (i te właśnie są podawane jako przykład).
Potwierdzają to wszystkie badania naukowe.