
Macierze – rozwiązywanie równań liniowych (Java)
Równania liniowe
Układ równań liniowych składa się z m równań i n niewiadomych. Możemy go przedstawić w postaci:
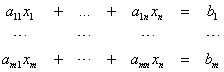
a – to znane współczynniki liczbowe
x – to niewiadome
b – to znane tzw. wyrazy wolne
Rozwiązanie układu równań polega na wyznaczeniu wartości ![]()
Metoda podstawiania
Tradycyjna metoda rozwiązywania równań znana każdemu, kto skończył przynajmniej gimnazjum.
Równanie:
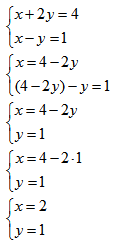
Metoda przeciwnych współczynników
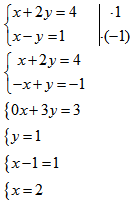
Metoda graficzna
Była omawiana w mojej książce Matematyka dla programistów Java.
Każde z równań wyznacza pewną prostą. Rozwiązanie równania to współrzędne punktu przecięcia obu linii wykreślonych w układzie współrzędnych.
Postać macierzowa
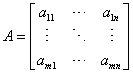
Równanie można przedstawić w postaci macierzy współczynników:
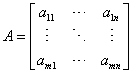
Wyrazy wolne można przedstawić w postaci wektora b albo macierzy kolumnowej B:
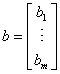 albo
albo 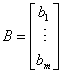
Niewiadome można przedstawić w postaci wektora x albo macierzy kolumnowej X:
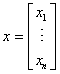 albo
albo 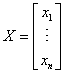
Cały układ możemy przedstawić jako:
![]() albo
albo ![]()
czyli
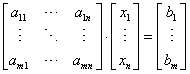
Układ równań liniowych można też przedstawić w postaci wektorowej:
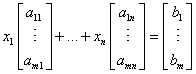
Ze względu na sposób obliczania często używa się tzw. macierzy uzupełnionej Ab układu równań ![]() :
:
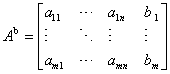
Rozwiązaniem układu jest wektor, którego składowe po wstawieniu w miejsce odpowiednich niewiadomych x i zsumowaniu dadzą elementy kolumny wyrazów wolnych.
Metoda eliminacji Gaussa – Jordana
Macierz uzupełnioną układu:
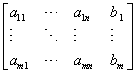
sprowadzamy do postaci bazowej:
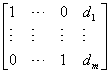
przy użyciu operacji elementarnych, z zastrzeżeniem, że nie można zmienić położenia kolumny wyrazów wolnych. Do operacji elementarnych nie wymienionych uprzednio dochodzi możliwość pominięcia równania tożsamościowego w układzie (równanie tożsamościowe to równanie mające nieskończenie wiele rozwiązań).
Układ równań:
![]()
zapisujemy jako macierz uzupełnioną:
![]()
Odejmujemy wiersz drugi od pierwszego:
![]()
Dzielimy wiersz pierwszy przez 3:
![]()
Dodajemy wiersz pierwszy do drugiego:
![]()
Zamieniamy wiersze miejscami:
![]()
Czyli:
![]()
Możemy tez użyć metody gaussJordan(Matrix) prezentowanej w klasie MatrixUtil.
Przykład zastosowania metody znajduje się w klasie Matrix079. Po uruchomieniu klasy na konsoli zobaczymy:
1.0 0.0 2.0 0.0 1.0 1.0
Jak widzimy – wynik jest jednakowy.
Istnienie rozwiązań
Układ równań liniowych może mieć rozwiązanie i wtedy nazywany jest układem zgodnym (niesprzecznym) albo może nie mieć rozwiązania i wtedy nazywany jest układem sprzecznym.
Układ zgodny może mieć dokładnie jedno rozwiązanie i wtedy nazywamy go układem oznaczonym albo nieskończenie wiele rozwiązań i wtedy nazywany jest układem nieoznaczonym.
| Układ zgodny (istnieje rozwiązanie) | Układ sprzeczny (nie istnieje rozwiązanie) | |
| Układ oznaczony (istnieje 1 rozwiązanie) | Układ nieoznaczony (istnieje ∞ wiele rozwiązań) | |
Twierdzenie Kroneckera – Capelliego
Układ równań liniowych jest zgodny (czyli ma rozwiązanie) wtedy i tylko wtedy, gdy rząd macierzy A współczynników układu jest równy rzędowi macierzy uzupełnionej U, czyli
![]()
Jeżeli ![]() układ jest sprzeczny (nie ma rozwiązania).
układ jest sprzeczny (nie ma rozwiązania).
Jeżeli rząd macierzy A i rząd macierzy U są równe liczbie niewiadomych n:
![]()
to układ taki ma dokładnie jedno rozwiązanie.
W przeciwnym wypadku:
![]()
układ ma nieskończenie wiele rozwiązań.
| Układ zgodny (istnieje rozwiązanie) |
Układ sprzeczny (nie istnieje rozwiązanie) |
|
| Układ oznaczony (istnieje 1 rozwiązanie) |
Układ nieoznaczony (istnieje ∞ wiele rozwiązań) |
|
W przypadku układu mającego nieskończenie wiele rozwiązań część niewiadomych przekształca się w parametry, które mogą przyjmować dowolne wielkości. W tym przypadku można zapisać tzw. rozwiązanie ogólne układu. Dopiero podanie konkretnego parametru/parametrów pozwala na wyznaczenie rozwiązania równania dla tego parametru, czyli uzyskanie tzw. rozwiązania szczególnego.
Rozwiązanie bazowe to rozwiązanie równania ogólnego, gdy wszystkie parametry (zmienne bazowe) przyjmują wartość 0. Niewiadome, które nie są parametrami nazywane są zmiennymi swobodnymi (nie bazowymi).
Liczba zmiennych swobodnych równa się rzędowi obu macierzy (ang. rank). Liczba parametrów (zmiennych bazowych) wynosi ![]() .
.
Mamy układ równań:
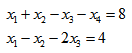
Zapisujemy układ w postaci macierzowej:
![]()
oraz w postaci rozszerzonej:
![]()
Sprawdzamy, że:
![]()
Liczba niewiadomych ![]()
a zatem układ ma rozwiązanie. Ponieważ ![]()
to układ ten ma nieskończenie wiele rozwiązań.
Rozwiązanie będzie zależne od
![]() parametrów.
parametrów.
Rozwiązanie tradycyjne
Przekształcamy równanie drugie aby otrzymać x1.
![]()
Podstawiamy x1 do równania pierwszego i otrzymujemy:
![]()
Podstawiamy x2 do pierwszego równania, aby obliczyć x1 i otrzymujemy:
![]()
Rozwiązaniem bazowym układu jest:
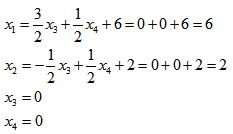
Mamy więc:
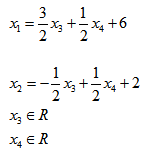
Jeżeli przyjmiemy np:
x3=2
x4=2
to łatwo obliczyć, że:
![]()
Jeżeli podstawimy te wartości do pierwotnych równań to otrzymamy:
![]()
czyli nasze obliczenia są prawidłowe.
Rozwiązanie Gaussa – Jordana
Metodą eliminacji Gaussa – Jordana sprowadzamy macierz do postaci schodkowej:
![]()
czyli równania:
![]()
Po rozwiązaniu tradycyjną metodą otrzymamy:
![]()
![]()
czyli te same równania.
Obie metody są niewygodne.
Rozwiązanie bazowe
Aby otrzymać rozwiązanie bazowe układu równań możemy użyć metody gaussJordan(Matrix, double ...) z klasy MatrixUtil.
Metoda sprawdza, czy układ jest sprzeczny, czy nie, a jeżeli nie jest – sprawdza, ile rozwiązań istnieje. Jeżeli istnieje jedno rozwiązanie, w ostatniej kolumnie macierzy wynikowej podane są wartości pierwiastków, a jeżeli wiele rozwiązań w ostatniej kolumnie podane jest rozwiązanie bazowe. Jeżeli podamy wartości paramValues dla których chcemy takie równanie rozwiązać – otrzymujemy w ostatniej rozwiązanie układu równań dla tych parametrów.
Przykład użycia tej metody jest podany w klasie Matrix080.
double[][] A = {{1, 1, -1, -1, 8},
{1, -1, -2, 0, 4}};
Matrix matrix = new Matrix(A);
matrix.printToConsole();
Util.print("");
Matrix mat = null;
try {
mat = MatrixUtil.gaussJordan(matrix,
new double[]{0, 0});
} catch (MatrixException e) {
e.printStackTrace();
}
mat.printToConsole();
Util.print("");
Po uruchomieniu klasy na konsoli zobaczymy:
1.0 1.0 -1.0 -1.0 8.0 1.0 -1.0 -2.0 0.0 4.0 1.0 0.0 0.0 0.0 6.0 0.0 1.0 0.0 0.0 2.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0
W klasie Matrix081 rozwiązany jest powyższy przykład dla parametrów: 2, 2.
double[][] A = {{1, 1, -1, -1, 8},
{1, -1, -2, 0, 4}};
Matrix matrix = new Matrix(A);
matrix.printToConsole();
Util.print("");
Matrix mat = null;
try {
mat = MatrixUtil.gaussJordan(matrix,
2, 2);
} catch (MatrixException e) {
e.printStackTrace();
}
mat.printToConsole();
Util.print("");
Po uruchomieniu klasy na konsoli zobaczymy:
1.0 1.0 -1.0 -1.0 8.0 1.0 -1.0 -2.0 0.0 4.0 1.0 0.0 0.0 0.0 10.0 0.0 1.0 0.0 0.0 2.0 0.0 0.0 1.0 0.0 2.0 0.0 0.0 0.0 1.0 2.0
Twierdzenie i wzory Cramera
Mamy układ równań:
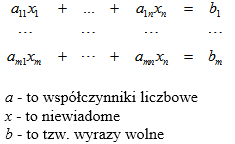
macierzą układu równań jest:
a macierz kolumnowa wyrazów wygląda tak:
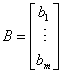
Każdą kolumnę w macierzy A możemy kolejno zastąpić przez macierz kolumnową B i możemy uzyskać n macierzy wynikowych od ![]() .
.
Jeżeli
![]()
to
![]()
i jedynym rozwiązaniem tego układu jest:
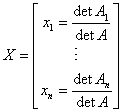
Mamy macierz:
![]()
oraz kolumnę wyrazów wolnych:
![]()
n = 2
rank A = 2 = n
czyli
![]() i istnieje tylko jedno rozwiązanie:
i istnieje tylko jedno rozwiązanie:
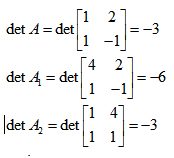
a więc:
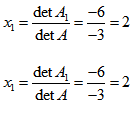
Do rozwiązania problemu możemy użyć metody cramer(Matrix, double[]) w klasie MatrixUtil.
Przykład w klasie Matrix082:
double[][] A = {{1, 2}, {1, -1}};
Matrix mat = new Matrix(A);
mat.printToConsole();
double[] B = {4, 1};
ArrayUtil.print(B);
double[] C = null;
try {
C = MatrixUtil.cramer(mat, B);
} catch (MatrixException e) {
e.printStackTrace();
}
ArrayUtil.print(C);
Po uruchomieniu klasy na konsoli zobaczymy:
1.0 2.0 1.0 -1.0 [4.0, 1.0] [2.0, 1.0]
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 025;

