
Macierze przekształceń elementarnych (1) (Java)
Dla każdej macierzy kwadratowej A możemy znaleźć taką macierz przekształcenia E, T albo I, że pomnożenie
lewostronne macierzy A przez macierz przekształcenia wykona odpowiednie przekształcenie na wierszach macierzy A, a pomnożenie prawostronne, wykona odpowiednie przekształcenie na wierszach A.
Macierz przekształcenia E
Macierz
![]()
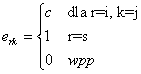
i – oznacza wiersz macierzy wyjściowej, do którego nastąpi dodanie
j – oznacza wiersz macierzy, który zostanie pomnożony przez c i dodany do i
c – oznacza stałą mnożenia
e – oznacza macierz przekształcenia (wyjściową)
r i k – oznaczają wiersz i kolumnę tej macierzy, gdzie należy umieścić mnożnik c. Gdy r=i oraz k=j wstawiamy tam mnożnik c, gdy r=k wstawiamy 1,
0 wstawiamy we wszystkich pozostałych miejscach
Podobnie wykonujemy operacje na kolumnach.
Mamy macierz:
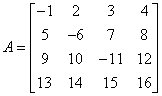
Wyznacznik tej macierzy wynosi:
![]()
Do wiersza drugiego dodajemy wiersz trzeci pomnożony przez 2:
![]()
i=2, j=3, c=2
Mnożnik c=2 umieszczamy w wierszu r=i=2 oraz w kolumnie k=j=3
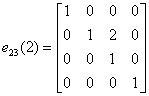
![]()
Jeżeli teraz pomnożymy
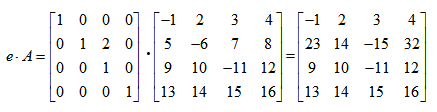
Przykład w klasie Matrix059:
1.0 0.0 0.0 0.0 0.0 1.0 2.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 x -1.0 2.0 3.0 4.0 5.0 -6.0 7.0 8.0 9.0 10.0 -11.0 12.0 13.0 14.0 15.0 16.0 -18752.0 = -1.0 2.0 3.0 4.0 23.0 14.0 -15.0 32.0 9.0 10.0 -11.0 12.0 13.0 14.0 15.0 16.0 -18752.0
Jeżeli chcemy wykonać operację na kolumnach (czyli do kolumny drugiej dodać wartość kolumny trzeciej pomnożonej przez dwa) musimy naszą wartość c umieścić w drugiej kolumnie i w trzecim wierszu oraz dokonać mnożenia prawostronnego:
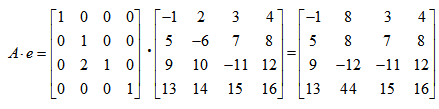
Przykład w klasie Matrix060:
-1.0 2.0 3.0 4.0 5.0 -6.0 7.0 8.0 9.0 10.0 -11.0 12.0 13.0 14.0 15.0 16.0 -18752.0 x 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 2.0 1.0 0.0 0.0 0.0 0.0 1.0 = -1.0 8.0 3.0 4.0 5.0 8.0 7.0 8.0 9.0 -12.0 -11.0 12.0 13.0 44.0 15.0 16.0 -18752.0
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 017;

