
Tworzenie macierzy przekształceń elementarnych (Java)
Dla każdej macierzy możemy stworzyć macierz odpowiedniego przekształcenia.
Mamy macierz:
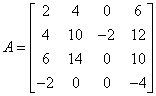
Wyznacznik tej macierzy wynosi:
![]()
Tworzenie macierzy E
Dla powyższej macierzy tworzymy macierz przekształcenia takiego, aby po jego wykonaniu w elemencie a1,1 pojawiło się zero. Najlepiej pomnożyć wiersz pierwszy przez 2 i wynik odjąć od wiersza drugiego.
Przy użyciu poniższej metody tworzymy macierz przekształcenia E:
Matrix matrix2 = MatrixUtil.makeE(matrix1, Elem.Row, 2, 1, -2);
Jest to macierz postaci:
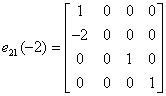
Po wykonaniu mnożenia e⋅A otrzymujemy macierz wynikową:
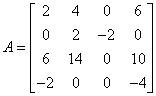
Przykład w klasie Matrix065:
double[][] array1 = {{2, 4, 0, 6}, {4, 10, -2, 12}, {6, 14, 0, 10},
{-2, 0, 0, -4}};
Matrix matrix1 = new Matrix(array1);
matrix1.printToConsole();
try {
Util.print(matrix1.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Matrix matrix2 = MatrixUtil.makeE(matrix1, Elem.Row, 1, 0, -2);
matrix2.printToConsole();
Util.print("");
Matrix matrix3 = MatrixUtil.multiply3(matrix2, matrix1);
matrix3.printToConsole();
try {
Util.print(matrix3.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Po uruchomieniu klasy na konsoli zobaczymy:
2.0 4.0 0.0 6.0 4.0 10.0 -2.0 12.0 6.0 14.0 0.0 10.0 -2.0 0.0 0.0 -4.0 144.0 1.0 0.0 0.0 0.0 -2.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 2.0 4.0 0.0 6.0 0.0 2.0 -2.0 0.0 6.0 14.0 0.0 10.0 -2.0 0.0 0.0 -4.0 144.0
Tworzenie macierzy T
Mamy macierz wynikową z poprzedniej operacji:
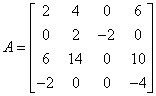
Chcemy zamienić kolumnę drugą z trzecią.
Używając poniższej metody tworzymy macierz przekształcenia T:
Matrix matrix2 = MatrixUtil.makeT(matrix1, 2, 3);
Jest to macierz:
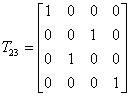
Po pomnożeniu prawostronnym A⋅T otrzymujemy macierz wynikową:
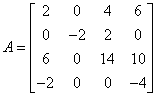
Przykład w klasie Matrix066:
double[][] array1 = {{2, 4, 0, 6}, {0, 2, -2, 0},
{6, 14, 0, 10}, {-2, 0, 0, -4}};
Matrix matrix1 = new Matrix(array1);
matrix1.printToConsole();
try {
Util.print(matrix1.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Matrix matrix2 = MatrixUtil.makeT(matrix1, 1, 2);
matrix2.printToConsole();
Util.print("");
Matrix matrix3 = MatrixUtil.multiply3(matrix1, matrix2);
matrix3.printToConsole();
try {
Util.print(matrix3.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Po uruchomieniu klasy na konsoli zoabczymy:
2.0 4.0 0.0 6.0 0.0 2.0 -2.0 0.0 6.0 14.0 0.0 10.0 -2.0 0.0 0.0 -4.0 144.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 1.0 2.0 0.0 4.0 6.0 0.0 -2.0 2.0 0.0 6.0 0.0 14.0 10.0 -2.0 0.0 0.0 -4.0 -144.0
Jak widzimy zmienił się znak wyznacznika.
Tworzenie macierzy I
Mamy macierz wynikową z poprzedniej operacji:
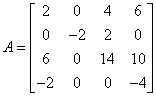
Nie mamy żadnego rozsądnego powodu, poza zwykłym kaprysem programisty, aby mnożyć którykolwiek wiersz macierzy. Pomnóżmy wiersz czwarty przez 3:
Macierz tego przekształcenia wygląda następująco:
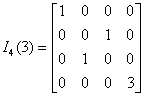
Mnożymy I⋅A
Otrzymujemy macierz wynikową:
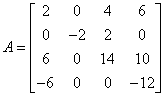
Przykład w klasie Matrix067:
double[][] array1 = {{2, 0, 4, 6}, {0, -2, 2, 0},
{6, 0, 14, 10}, {-2, 0, 0, -4}};
Matrix matrix1 = new Matrix(array1);
matrix1.printToConsole();
try {
Util.print(matrix1.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Matrix matrix2 = MatrixUtil.makeI(matrix1, 3, 3);
matrix2.printToConsole();
Util.print("");
Matrix matrix3 = MatrixUtil.multiply3(matrix2, matrix1);
matrix3.printToConsole();
try {
Util.print(matrix3.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Po uruchomieniu kodu na konsoli zobaczymy:
2.0 0.0 4.0 6.0 0.0 -2.0 2.0 0.0 6.0 0.0 14.0 10.0 -2.0 0.0 0.0 -4.0 -144.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 3.0 2.0 0.0 4.0 6.0 0.0 -2.0 2.0 0.0 6.0 0.0 14.0 10.0 -6.0 0.0 0.0 -12.0 -432.0
Jak widzimy wyznacznik został pomnożony przez 3.
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 020;

