Test zgodności Χ² jako test losowości

Test zgodności Χ2 jako test losowości

Test zgodności χ² przy wyszczególnionych parametrach rozkładu

Test będzie nam służył do badania losowości kluczy kryptograficznych.

Najprostszą miarą odchyleń rozkładu w próbie od rozkładu zakładanego jest wielkość obliczona z wzoru:

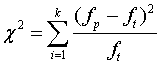
gdzie:

oznacza liczebność z próby

oznacza liczebność oczekiwaną

k oznacza liczbę badanych grup

Liczba stopni swobody

Liczebność nie może być mniejsza od 5 (niektórzy autorzy przyjmują 10). Jeżeli liczebność jest mniejsza, należy zsumować sąsiednie liczebności, tak aby otrzymać (lub 10).

Jeżeli odczytane z tablicy dla stopni swobody, przy zakładanym poziomie istotności α hipotezę o zgodności rozkładu z próby z zakładanym odrzucamy.

Jeżeli nie ma podstaw do odrzucenia hipotezy.

Jeżeli obliczamy wartość:

i wartość tę porównujemy z krytycznymi wartościami w rozkładzie t Studenta przy założonym poziomie istotności α i dla liczby stopni swobody.

Tab. Wartości krytyczne w teście

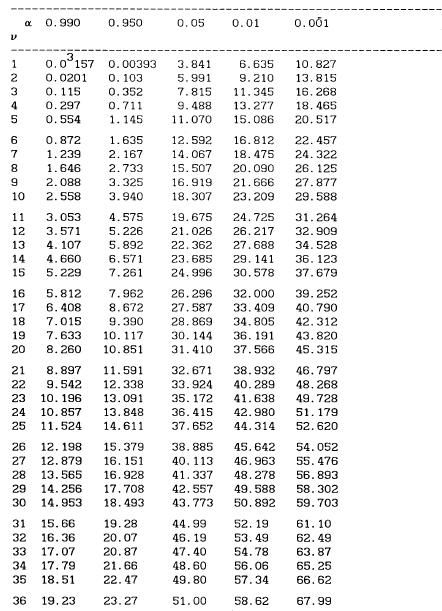
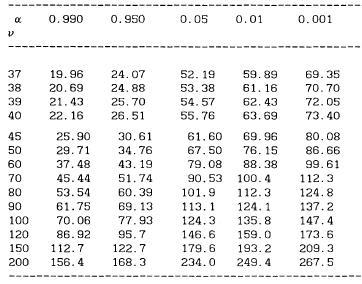
Przykład

W doświadczeniach genetycznych nad dziedziczeniem wzoru użyłkowania skrzydeł (A i B) oraz zabarwienia czułek (C i D) uzyskano następujące rozszczepienie cech:

120 osobników z cechą A i C

48 osobników z cechą A i D

36 osobników z cechą B i C

13 osobników z cechami B i D

przy zakładanym stosunku 9:3:3:1

Na poziomie istotności zweryfikować hipotezę, że wyniki doświadczenia są zgodne z teorią (czyli, że rozszczepienie cech ma zakładany stosunek (9:3:3:1).

Obliczenia przeprowadzamy w tabeli:

	liczebność w próbie	prawdopodobieństwo zakładane	Liczebność oczekiwana
AC	120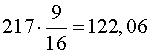
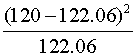AD	48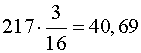
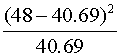BC	36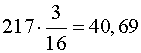
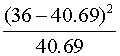BD	13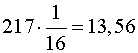
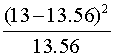k=4	217			Suma = 1,912

przy i stopniach swobody (odczytane z tablic). Ponieważ obliczonego nie ma podstaw do odrzucenia hipotezy. Wyniki doświadczenia są zgodne z teorią.

Klasy

Klasa TestZgodnosci.java

package crypto.vigenere;
public class TestZgodnosci{
	private static final int[] freqZaklad = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1};
	private static final int sum = sum(freqZaklad);
	private static final int k = freqZaklad.length;//liczba badanych grup
    private final int[] freqSample;//czestosc z proby
    private double chi;
	public TestZgodnosci(int[] freqSample){
		this.freqSample = freqSample;
		int n = sum(freqSample);
        //prawdopodobienstwa zakladane
        double[] probabZaklad = new double[k];
        //czestosci oczekiwane
        double[] freqOczek = new double[k];
		chi = 0.0;
		for(int i = 0; i < k; i++){
			probabZaklad[i] = (double)freqZaklad[i] / (double)sum;
			freqOczek[i] = n * probabZaklad[i];
			chi += Math.pow(freqSample[i] - freqOczek[i], 2) / freqOczek[i];
		}
	}
	public double getChi() {
		return chi;
	}
	private static int sum(int[] tabl) {
		int sum = 0;
		for (int value : tabl) {
			sum += value;
		}
		return sum;
	}
	public int[] getFreqSample() {
		return freqSample;
	}
}

Crypto05

package crypto.vigenere;
public class Crypto05 {
    public static void main(String[] args){
        int[] tabl = {120,48,36,13};
        TestZgodnosci tx = new TestZgodnosci(tabl);
        double chi = tx.getChi();
        System.out.println(chi);
    }
}

W klasie TestZgodnosci ustawiamy
private static final int[]freqZaklad = {9,3,3,1};
Po uruchomieniu klasy Crypto05 otrzymujemy wynik na konsoli:

1.9124423963133639

2019-06-23 16:26:52