Test serii jako test losowości

Test serii jako test losowości

Ten test będzie nam służył do oceny losowości klucza kryptograficznego.

W tym teście z populacji generalnej o dowolnym rozkładzie pobieramy próbę n elementów. Sprawdzamy hipotezę, że sposób pobierania próby (doboru elementów) jest losowy.

Tworzymy ciąg uporządkowany wedułg kolejności pobierania elementów. Obliczamy medianę z próby. Każdemu wynikowi mniejszemu od mediany przypisujemy symbol A, a większemu od niej – symbol B.

Liczba elementów , liczba elementów . Wyniki równe medianie odrzucamy. W ten sposób otrzymujemy n-elementowy ciąg mieszany () składający się z symboli A i B. Obliczamy liczbę u serii.

Np. w ciągu:

A BB AA BBB AAAA B AA B

liczba serii

Jeżeli hipoteza o losowości próby jest prawdziwa, liczba serii u powinna być zgodna z rozkładem tabelarycznym. W oparciu o ten rozkład tworzymy dwustronny obszar krytyczny odczytując

przy 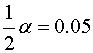oraz przy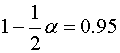

Wartość empiryczną u porównujemy z i .

Jeżeli zachodzi nierówność:

albo hipotezę o losowości próby odrzucamy.

Jeżeli:

nie mamy podstaw do odrzucenia hipotezy o losowości próby, czyli hipotezę o losowości próby przyjmujemy.

Tab. 1A. Wartości krytyczne w teście serii dla poziomu ufności

 

Tab. 1B. Wartości krytyczne w teście serii dla poziomu ufności

Przykład

Po otwarciu ula złapano kolejno pierwsze 15 pszczół, które wyleciały. Zbadano ciężar ich ciała. Miały one następujące ciężary, ustawione według kolejności wylatywania:

37, 40, 36, 39, 38, 43, 46, 50, 49, 55, 48, 32, 56, 62, 53

Na poziomie istotności zweryfikować hipotezę, że taki dobór pszczół jest losowy.

Porządkujemy wyniki, aby obliczyć medianę z próby:

32, 36, 37, 38, 39, 40, 43, 46, 48, 49, 50, 53, 55, 56, 62

mediana = 46

Symbolem A oznaczamy wyniki mniejsze od mediany, symbolem B wyniki większe od mediany. Wynik równe medianie pomijamy:

37	40	36	39	38	43	46	50	49	55	48	3	56	62	53
A	A	A	A	A	A		B	B	B	B	A	B	B	B

Otrzymaliśmy 4 serie:

AAAAAA BBBB A BBB

Z tab. 1A odczytujemy:

przy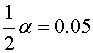

Z tab. 1B odczytujemy: przy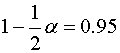

Ponieważ hipotezę o losowości próby odrzucamy. Z ula wylatywały najpierw osobniki lżejsze, o większej ruchliwości.

Przy większej liczebności próby, gdy n₁ i n₂ są większe od 20 można zastosować aproksymację rozkładem normalnym – obliczamy:

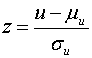
gdzie:

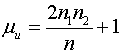
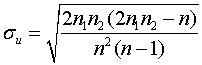
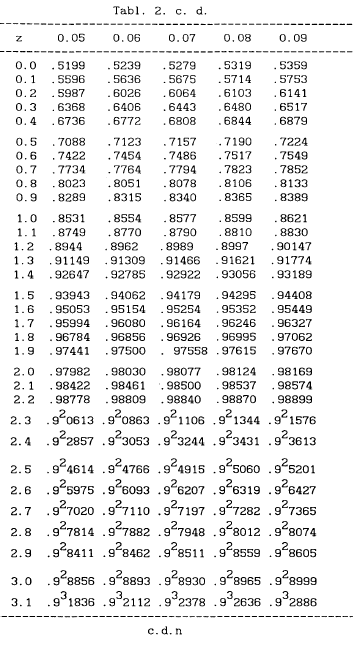
Obliczoną wartość porównujemy z wartościami odczytanymi z tab. 2.

Klasy

Klasa TestSerii.java

package crypto.vigenere;
import java.util.*;
public class TestSerii{
	private final String liczba;
	private int u = 0;
	private int A = 0;
	private int B = 0;
	private double z = 0;
	private final double mediana;
	public TestSerii(String liczba){
		this.liczba = liczba;
		int len = liczba.length();
		int[] tokeny = tokenize(liczba);
		int[] tokenySort = tokeny.clone();
		mediana = median2(tokenySort);
		StringBuilder st = new StringBuilder();
		for(int i = 0; i < len; i++){
			if(tokeny[i] < mediana){
				st.append("A");
			}
			else if(tokeny[i] > mediana){
				st.append("B");
			}
		}
		String seria = st.toString();
		String prev = "";
		String now;
		for(int i = 0; i < seria.length(); i++){
			now = seria.substring(i, i + 1);
			if(now.equals("A")){
				A++;
			}
			else{
				B++;
			}
			if(!prev.equals(now)){
				u++;
				prev = now;
			}
		}
		if((A > 20) && (B > 20)){
			double sigma = Math.sqrt((2 * A * B * (2 * A * B - (A + B)))
					/ Math.pow(A * B, 2) * ((A + B - 1)));
			double mi = ((2 * A * B) / (A + B)) + 1.0;
			z = (u - mi) / sigma;
		}
	}
	private static int[] tokenize(String liczba) {
		int len = liczba.length();
		int[] toks = new int[len];
		for(int i = 0; i < len; i++){
			toks[i] = Integer.parseInt(liczba.substring(i, i + 1));
		}
		return toks;
	}
	//oblicza mediane
	public static double median2(int[] array) {
		Arrays.sort(array);
		int len = array.length;
		double value;
		if(len % 2 == 0){
			value = ((double)array[(len + 1) / 2] + (double)array[(len + 1) / 2 + 1]) / 2;
		}
		else{
			value = array[(len + 1) / 2];
		}
		return value;
	}
	public String getLiczba() {
		return liczba;
	}
	public int getU() {
		return u;
	}
	public int getA() {
		return A;
	}
	public int getB() {
		return B;
	}
	public double getZ() {
		return z;
	}
	public double getMediana() {
		return mediana;
	}
}

Klasa Crypto06.java

package crypto.vigenere;
import java.math.*;
public class Crypto06 {
    public static void main(String[] args) {
        FrequencyMap<String> map = new FrequencyMap<>();
        //generujemy 100 liczb po 100 cyfr
        String[] tab = Generator.generuj(10, 200, map);
        for (String s : tab) {
            System.out.println(s);
        }
        //sprawdzamy rozklad cyfr we wszystkich 100 liczbach lącznie
        int[] freq = map.printAll();
        //wykonujemy test losowosci rozkladu
        TestZgodnosci test = new TestZgodnosci(freq);
        System.out.println("chi: " + test.getChi());
        //wybieramy liczbe ze srodka
        String liczba = tab[tab.length / 2];
        //wykonujemy test losowosci liczby
        TestSerii ts = new TestSerii(liczba);
        System.out.println("liczba: " + liczba);
        System.out.println("mediana: " + ts.getMediana());
        System.out.println("u: " + ts.getU());
        System.out.println("A: " + ts.getA());
        System.out.println("B: " + ts.getB());
        System.out.println("z: " + ts.getZ());
        //znajdujemy liczbe pierwsza, ktora jest wieksza od tej liczby
        BigInteger big = new BigInteger(liczba);
        BigInteger prime = big.nextProbablePrime();
        System.out.println(prime);
    }
}

Wyniki

Plik: Crypto05.java.

Rozkład cyfr w tych liczbach wynosi:

0 98

1 93

2 94

3 103

4 117

5 110

6 96

7 94

8 89

9 106

Testem zgodności badamy czy rozkład liczb jest losowy (w tym przypadku równomierny):

chi: 6.960000000000001 przy 10 – 1 = 9 stopniach swobody.

dla stopni swobody wynosi 16.919

Ponieważ nie mamy podstaw do odrzucenia hipotezy, że rozkład jest równomierny, czyli rozkład jest równomierny.

Bierzemy środkową liczbę:

85011723206741980364416789436094187999442602373
  09593038912574809353749675078
    755249379734314934854264

Wykonujemy test serii dla tej liczby:

mediana: 4.5

u: 50

A: 51

B: 49

z: 0.0

Wartość z porównana z tablicami mówi nam, że hipotezy o losowości próby nie możemy odrzucić, czyli rozkład jest losowy.

Jeżeli chcemy mieć liczbę pierwszą to znajdujemy pierwszą liczbę pierwszą, większą od tej liczby:

BigInteger big = new BigInteger(liczba);
BigInteger prime = big.nextProbablePrime();

85011723206741980364416789436094187999442602373
  09593038912574809353749675078
    755249379734314934855901

Teraz warto byłoby przetestować jej pierwszość testem Millera-Rabina, ale nie załączam stosownych algorytmów. Moim celem nie jest tworzenie szyfrów doskonałych lecz pokazanie zgrubnie pracy z testami.

2019-06-28 19:00:20