Odbicie względem prostej nie przechodzącej przez punkt (0,0) (2) (HTML5 canvas)

Odbicie względem prostej nie przechodzącej przez punkt (0,0)

Użyty został skrypt transform.js.

Przypadek 2

Prosta nie jest równoległa do osi Y i może być przedstawiona równaniem y=mx+b

Prosta przechodzi przez dwa punkty (160,0) i (260,250).

tgφ=250/100=2,5=m;

Równanie prostej to y=2.5x-400, czyli b=-400

Zawartość możesz zobaczyć w
przeglądarce obsługującej element <canvas>
z kontekstem "2d"

Listing

	var cv = document.getElementById("canvas");
	var ctx = cv.getContext("2d");
	ctx.beginPath();
	ctx.moveTo(160,0);
	ctx.lineTo(260,250);
	ctx.strokeStyle = "black";
	ctx.stroke();
	var leftX = 220;
	var topY = 20;
	var width = 100;
	var height = 75;
	var cornerRadius = 15;
	drawRectangle(ctx);
	

Wykonujemy kolejne kroki:

translacja figury o współczynnik b/m=-400/2.5=-160

Prosta przechodzi teraz przez punkt (0,0).

Zawartość możesz zobaczyć w
przeglądarce obsługującej element <canvas>
z kontekstem "2d"

Listing

	var cv = document.getElementById("canvas1");
	var ctx = cv.getContext("2d");
	ctx.save();
	ctx.beginPath();
	ctx.translate(-160,0);
	ctx.moveTo(160,0);
	ctx.lineTo(260,250);
	ctx.strokeStyle = "black";
	ctx.stroke();
	ctx.restore();
	var leftX = 220;
	var topY = 20;
	var width = 100;
	var height = 75;
	var cornerRadius = 15;
	ctx.translate(-160,0);
	drawRectangle(ctx);
	

odbicie figury względem przesuniętej linii

Macierz odbicia wygląda tak:

,

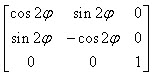gdzie φ jest kątem pod jakim prosta przecina oś X.

Zawartość możesz zobaczyć w
przeglądarce obsługującej element <canvas>
z kontekstem "2d"

Listing

	var cv = document.getElementById("canvas2");
	var ctx = cv.getContext("2d");
	ctx.save();
	ctx.beginPath();
	ctx.translate(-160,0);
	ctx.moveTo(160,0);
	ctx.lineTo(260,250);
	ctx.strokeStyle = "black";
	ctx.stroke();
	ctx.restore();
	var leftX = 220;
	var topY = 20;
	var width = 100;
	var height = 75;
	var cornerRadius = 15;
	ctx.transform(Math.cos(2*Math.atan(2.5)),Math.sin(2*Math.atan(2.5)),Math.sin(2*Math.atan(2.5)),-Math.cos(2*Math.atan(2.5)),0,0);
	ctx.translate(-160,0);
	drawRectangle(ctx);
	

translacja powrotna

Zawartość możesz zobaczyć w
przeglądarce obsługującej element <canvas>
z kontekstem "2d"

Listing

	var cv = document.getElementById("canvas3");
	var ctx = cv.getContext("2d");
	ctx.save();
	ctx.beginPath();
	ctx.moveTo(160,0);
	ctx.lineTo(260,250);
	ctx.strokeStyle = "black";
	ctx.stroke();
	ctx.restore();
	var leftX = 220;
	var topY = 20;
	var width = 100;
	var height = 75;
	var cornerRadius = 15;
	ctx.translate(160,0);
	ctx.transform(Math.cos(2*Math.atan(2.5)),Math.sin(2*Math.atan(2.5)),Math.sin(2*Math.atan(2.5)),-Math.cos(2*Math.atan(2.5)),0,0);
	ctx.translate(-160,0);
	drawRectangle(ctx);