Macierze – przekształcenia elementarne (Java)

Macierze – operacje elementarne (Java)

Operacje elementarne

Operacje elementarne na macierzach to takie przekształcenia macierzy, które przekształcają daną macierz w macierz równoważną, czyli mającą taki sam zbiór rozwiązań.

Operacje elementarne to:

1. Dodanie do rzędu (albo) innego rzędu (albo kolumny) pomnożonego (pomnożonej) przez liczbę różną od zera
   (właściwość wyznacznika 6). Tę operację oznaczymy jako E
2. Zamiana dwóch rzędów (albo kolumn) miejscami (właściwość wyznacznika 2). Tę operację oznaczymy jako T
3. Pomnożenie rzędu (albo kolumny) przez dowolną liczbę różną od zera (właściwość wyznacznika 4). Tę operację oznaczymy jako I

Operacja E

Mamy macierz:

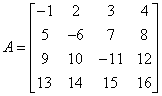
Wyznacznik tej macierzy wynosi

Do wiersza drugiego dodajemy wiersz trzeci pomnożony przez 2:

Nasza macierz wygląda teraz tak:

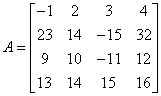
Jak widzimy wyznacznik nie zmienił się (Klasa Matrix056):

        double[][] array1 = {{-1, 2, 3, 4}, {5, -6, 7, 8},
               {9, 10, -11, 12}, {13, 14, 15, 16}};
        Matrix matrix1 = new Matrix(array1);
        matrix1.printToConsole();
        try {
            Util.print(matrix1.det());
        } catch (MatrixException e) {
            e.printStackTrace();
        }
        double[][] array2 = {{-1, 2, 3, 4}, {23, 14, -15, 32},
                {9, 10, -11, 12}, {13, 14, 15, 16}};
        Matrix matrix2 = new Matrix(array2);
        matrix2.printToConsole();
        try {
            Util.print(matrix2.det());
        } catch (MatrixException e) {
            e.printStackTrace();
        }

Po uruchomieniu klasy na konsoli zobaczymy:

-1.0 2.0 3.0 4.0
5.0 -6.0 7.0 8.0
9.0 10.0 -11.0 12.0
13.0 14.0 15.0 16.0
-18752.0
-1.0 2.0 3.0 4.0
23.0 14.0 -15.0 32.0
9.0 10.0 -11.0 12.0
13.0 14.0 15.0 16.0
-18752.0

Operacja T

Mamy macierz:

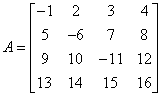
Wyznacznik tej macierzy wynosi

Zamieniamy miejscami wiersz 2 i 3:

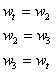
Nasza macierz wygląda teraz tak:

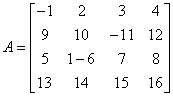
Jak widzimy zmienił się znak wyznacznika zgodnie z właściwością 6 wyznacznika (Klasa Matrix057):

 double[][] array1 = {{-1, 2, 3, 4}, {5, -6, 7, 8}, {9, 10, -11, 12},
                {13, 14, 15, 16}};
        Matrix matrix1 = new Matrix(array1);
        matrix1.printToConsole();
        try {
            Util.print(matrix1.det());
        } catch (MatrixException e) {
            e.printStackTrace();
        }
        double[][] array2 = {{-1, 2, 3, 4}, {9, 10, -11, 12}, {5, -6, 7, 8},
                {13, 14, 15, 16}};
        Matrix matrix2 = new Matrix(array2);
        matrix2.printToConsole();
        try {
            Util.print(matrix2.det());
        } catch (MatrixException e) {
            e.printStackTrace();
        }

Po uruchomieniu klasy na konsoli zobaczymy:

-1.0 2.0 3.0 4.0
5.0 -6.0 7.0 8.0
9.0 10.0 -11.0 12.0
13.0 14.0 15.0 16.0
-18752.0
-1.0 2.0 3.0 4.0
9.0 10.0 -11.0 12.0
5.0 -6.0 7.0 8.0
13.0 14.0 15.0 16.0
18752.0

Operacja I

Mamy macierz:

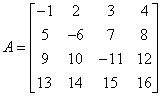
Mnożymy drugi wiersz przez 2.

Otrzymujemy następującą macierz:

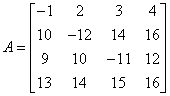
Jak widzimy wyznacznik został pomnożony przez tę samą liczbę, czyli 2 (Klasa Matrix058):

        double[][] array1 = {{-1, 2, 3, 4}, {5, -6, 7, 8}, {9, 10, -11, 12},
                {13, 14, 15, 16}};
        Matrix matrix1 = new Matrix(array1);
        matrix1.printToConsole();
        try {
            Util.print(matrix1.det());
        } catch (MatrixException e) {
            e.printStackTrace();
        }
        double[][] array2 = {{-1, 2, 3, 4}, {10, -12, 14, 16},
                {9, 10, -11, 12}, {13, 14, 15, 16}};
        Matrix matrix2 = new Matrix(array2);
        matrix2.printToConsole();
        try {
            Util.print(matrix2.det());
        } catch (MatrixException e) {
            e.printStackTrace();
        }

Po uruchomieniu klasy na konsoli zobaczymy:

-1.0 2.0 3.0 4.0
5.0 -6.0 7.0 8.0
9.0 10.0 -11.0 12.0
13.0 14.0 15.0 16.0
-18752.0
-1.0 2.0 3.0 4.0
10.0 -12.0 14.0 16.0
9.0 10.0 -11.0 12.0
13.0 14.0 15.0 16.0
-37504.0

Pliki do ściągnięcia

matrices016.zip

Moduł matrices – aktualny stan projektu = 016;

2019-11-21 09:25:40