
Macierze przekształceń elementarnych (3) (Java)
Dla każdej macierzy kwadratowej A możemy znaleźć taką macierz przekształcenia E, T albo I, że pomnożenie lewostronne macierzy A przez macierz przekształcenia wykona odpowiednie przekształcenie na wierszach macierzy A, a pomnożenie prawostronne, wykona odpowiednie przekształcenie na wierszach A.
Macierz przekształcenia I
![]()
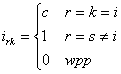
i – to numer mnożonego wiersza w macierzy wejściowej
c – stała, przez którą mnoży się rząd w macierzy wejściowej
r,k – to wiersz i kolumna macierzy wyjściowej
Mamy macierz:
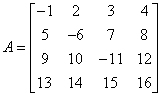
Wyznacznik macierzy wynosi:
![]()
Chcemy pomnożyć wiersz drugi przez 3:
![]()
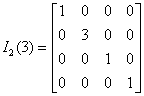
![]()
Mnożymy
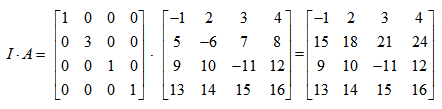
Pomnożyliśmy wiersz drugi przez 3. Zmieniła się wartość wyznacznika (×3).
Przykład w klasie Matrix063:
double[][] array1 = {{1, 0, 0, 0}, {0, 3, 0, 0},
{0, 0, 1, 0}, {0, 0, 0, 1}};
Matrix matrix1 = new Matrix(array1);
matrix1.printToConsole();
Util.print("x");
double[][] array2 = {{-1, 2, 3, 4}, {5, -6, 7, 8},
{9, 10, -11, 12}, {13, 14, 15, 16}};
Matrix matrix2 = new Matrix(array2);
matrix2.printToConsole();
try {
Util.print(matrix2.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Util.print("=");
Matrix matrix3 = MatrixUtil.multiply3(matrix1, matrix2);
matrix3.printToConsole();
try {
Util.print(matrix3.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Po uruchomieniu klasy na konsoli zobaczymy:
1.0 0.0 0.0 0.0 0.0 3.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 x -1.0 2.0 3.0 4.0 5.0 -6.0 7.0 8.0 9.0 10.0 -11.0 12.0 13.0 14.0 15.0 16.0 -18752.0 = -1.0 2.0 3.0 4.0 15.0 -18.0 21.0 24.0 9.0 10.0 -11.0 12.0 13.0 14.0 15.0 16.0 -56256.0
Aby uczynić to samo dla drugiej kolumny odwracamy kolejność mnożenia:

Pomnożyliśmy kolumnę drugą przez 3. Zmieniła się wartość wyznacznika (*times;3).
Przykład w klasie Matrix064:
double[][] array2 = {{-1, 2, 3, 4}, {5, -6, 7, 8},
{9, 10, -11, 12}, {13, 14, 15, 16}};
Matrix matrix2 = new Matrix(array2);
matrix2.printToConsole();
try {
Util.print(matrix2.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Util.print("x");
double[][] array1 = {{1, 0, 0, 0}, {0, 3, 0, 0}, {0, 0, 1, 0},
{0, 0, 0, 1}};
Matrix matrix1 = new Matrix(array1);
matrix1.printToConsole();
Util.print("=");
Matrix matrix3 = MatrixUtil.multiply3(matrix2, matrix1);
matrix3.printToConsole();
try {
Util.print(matrix3.det());
} catch (MatrixException e) {
e.printStackTrace();
}
Po uruchomieniu klasy na konsoli zobaczymy:
-1.0 2.0 3.0 4.0 5.0 -6.0 7.0 8.0 9.0 10.0 -11.0 12.0 13.0 14.0 15.0 16.0 -18752.0 x 1.0 0.0 0.0 0.0 0.0 3.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 1.0 = -1.0 6.0 3.0 4.0 5.0 -18.0 7.0 8.0 9.0 30.0 -11.0 12.0 13.0 42.0 15.0 16.0 -56256.0
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 019;

