
Kule i urny
W kombinatoryce często rozpatruje się różne możliwości rozkładu elementów przyjmując za przykład rozmieszczenie n kul w k urnach, przy wzięciu pod uwagę czy urna może być pusta czy nie.
Jest to równoznaczne z badaniem rozkładu n elementów mogących przyjmować k stanów, przy wzięciu pod uwagę czy dany stan może nie być reprezentowany przez żaden z elementów.
| Czy rozróżnialne są | Czy urna może być pusta | Oznaczenie | Podrozdział | |
|---|---|---|---|---|
| kule? | urny? | |||
| nie | nie | nie | R000 | Rozmieszczenie 1 |
| tak | R001 | Rozmieszczenie 2 | ||
| tak | nie | R010 | Rozmieszczenie 3 | |
| tak | R011 | Rozmieszczenie 4 | ||
| tak | nie | nie | R100 | Rozmieszczenie 5 |
| tak | R101 | Rozmieszczenie 6 | ||
| tak | nie | R110 | Rozmieszczenie 7 | |
| tak | R111 | Rozmieszczenie 8 | ||
W symbolu R indeks 1 oznacza 'tak, 0 oznacza 'nie’. Indeksy dotyczą kolejno: kul, urn i wypełnienia urny.
Rozmieszczenia oznaczone kolorem będą nas szczególnie interesowały w dalszych rozważaniach.
Rozmieszczenie 1
Kule nierozróżnialne (0). Urny nierozróżnialne (0). Urna nie może być pusta (0).
Wzór
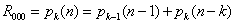
gdzie:
p oznacza liczbę partycji
Zadanie
Na ile sposobów możemy rozmieścić 4 nierozróżnialne kule w trzech nierozróżnialnych urnach. Urny nie mogą być puste.
Rozwiązanie
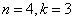
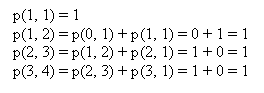
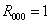
Sprawdzenie
| Lp | u | u | u |
|---|---|---|---|
| 1 |  |
 |
  |
Przykład
W klasie R000Main.java
n: 4 k: 3 r000(3,4) = 1
Rozmieszczenie 2
Kule nierozróżnialne (0). Urny nierozróżnialne (0). Urna może być pusta (1).
Wzór
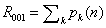
gdzie:
p – oznacza partycję
Zadanie
Na ile sposobów możemy rozmieścić 4 nierozróżnialne kule w czterech nierozróżnialnych urnach. Urny mogą być puste.
Rozwiązanie
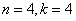
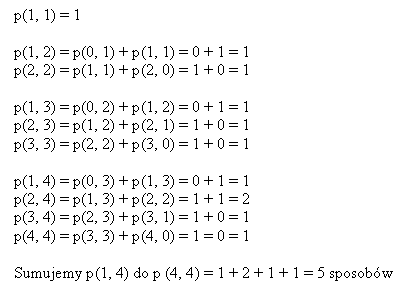
Sprawdzenie
| Lp | u | u | u | u |
|---|---|---|---|---|
| 1 |     |
|||
| 2 |    |
 |
||
| 3 |   |
  |
||
| 4 |   |
 |
 |
|
| 5 |  |
 |
 |
 |
Przykład
W klasie R001Main.java
n: 4 k: 4 r001(4,4) = 5
Rozmieszczenie 3
Kule nierozróżnialne (0). Urny rozróżnialne (1). Urna nie może być pusta (0).
Wzór
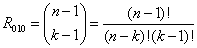
Zadanie
Na ile sposobów możemy rozmieścić 4 nierozróżnialne kule w 3 rozróżnialnych urnach. Urna nie może być pusta.
Rozwiązanie
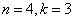
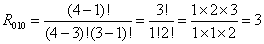
Sprawdzenie
| Lp. | u1 | u2 | u3 |
|---|---|---|---|
| 1 |  |
   |

|
| 2 |  |
 |
  |
| 3 |   |
 |
 |
Przykład
W klasie R010Main.java
n: 4 k: 3 r010(3,4) = 3
Rozmieszczenie 4
Kule nierozróżnialne (0). Urny rozróżnialne (1). Urna może być pusta (1).
Wzór
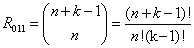
Zadanie
Na ile sposobów można rozmieścić 4 nierozróżnialne kule w 3 rozróżnialnych urnach, zakładając, że urna może być pusta.
Rozwiązanie
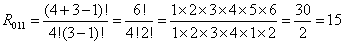
Sprawdzenie
| Lp | u1 | u2 | u3 |
|---|---|---|---|
| 1 |     |
||
| 2 |     |
||
| 3 |     |
||
| 4 |    |
 |
|
| 5 |    |
 |
|
| 6 |  |
   |
|
| 7 |    |
 |
|
| 8 |  |
   |
|
| 9 |  |
   |
|
| 10 |   |
  |
|
| 11 |   |
  |
|
| 12 |   |
  |
|
| 13 |  |
  |

|
| 14 |  |
 |
  |
| 15 |   |
 |
 |
Przykład
W pliku R011Main.java
n: 4 k: 3 r011(3,4) = 15
Rozmieszczenie 5
Kule rozróżnialne (1). Urny nierozróżnialne (0). Urna nie może być pusta (0).
Wzór
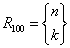
gdzie:
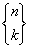
jest symbolem liczby Stirlinga.
Zadanie
Na ile sposobów można rozmieścić 4 rozróżnialne kule w 2 nierozróżnialnych urnach. Urna nie może być pusta.
Rozwiązanie
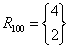
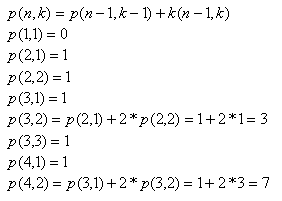
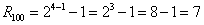
Sprawdzenie
| Lp | u | u |
|---|---|---|
| 1 |    |
 |
| 2 |    |
 |
| 3 |    |
 |
| 4 |    |
 |
| 5 |   |
  |
| 6 |   |
  |
| 7 |   |
  |
Przykład
W pliku R100Main.java
n: 4 k: 2 r100(2,4) = 7
Rozmieszczenie 6
Kule rozróżnialne (1). Urny nierozróżnialne (0). Urna może być pusta (1).
Wzór
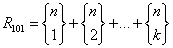
gdzie:
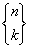
jest symbolem liczby Stirlinga.
Zadanie
Na ile sposobów można rozmieścić 4 rozróżnialne kule w 2 nierozróżnialnych urnach. Urna może być pusta.
Rozwiązanie
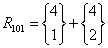
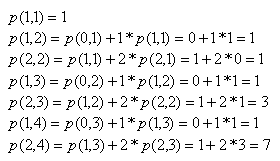
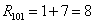
Sprawdzenie
| Lp | u | u |
|---|---|---|
| 1 |     |
|
| 2 |    |
 |
| 3 |
   |

|
| 4 |    |
 |
| 5 |
   |

|
| 6 |  
|
 
|
| 7 |
  |
  |
| 8 |   |
  |
Przykład
W pliku R101Main.java
n: 4 k: 2 r101(2,4) = 8
Rozmieszczenie 7
Kule rozróżnialne (1). Urny rozróżnialne (1). Urna nie może być pusta (0).
Wzór
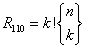
gdzie:
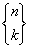
jest symbolem liczby Stirlinga.
Zadanie
Na ile sposobów można rozmieścić 3 rozróżnialne kule w 2 rozróżnialnych urnach. Urna nie może być pusta.
Rozwiązanie
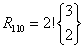
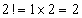
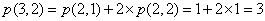
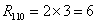
Sprawdzenie
| Lp. | u1 | u2 |
|---|---|---|
| 1 |   |
 |
| 2 |   |
 |
| 3 |  
|
 |
| 4 |  |
  |
| 5 |  |
  |
| 6 |  |
  |
Przykład
W klasie R110Main.java
n: 3 k: 2 r110(2,3) = 6
Rozmieszczenie 8
Kule rozróżnialne (1). Urny rozróżnialne (1). Urna może być pusta (1).
Wzór
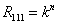
Zadanie
Na ile sposobów można rozmieścić 3 rozróżnialne kule w 3 rozróżnialnych urnach? Urny mogą być puste.
Rozwiązanie
n=3, k=3
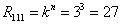
Sprawdzenie
| Lp. | u1 | u2 | u3 |
|---|---|---|---|
| 1 |    |
||
| 2 |    |
||
| 3 |    |
||
| 4 |   |
 |
|
| 5 |   |
 |
|
| 6 |  |
  |
|
| 7 |   |
 |
|
| 8 |  |
  |
|
| 9 |  |
  |
|
| 10 |   |
 |
|
| 11 |   |
 |
|
| 12 |  |
  |
|
| 13 |   |
 |
|
| 14 |  |
  |
|
| 15 |  |
  |
|
| 16 |   |
 |
|
| 17 |   |
 |
|
| 18 |  |
  |
|
| 19 |  
|
 |
|
| 20 |  |
  |
|
| 21 |  |
  |
|
| 22 |  |
 |
 |
| 23 |  |
 |
 |
| 24 |  |
 |
 |
| 25 |  |
 |
 |
| 26 |  |
 |
 |
| 27 |  |
 |
 |
Przykład
W klasie R111Main.java
n: 3 k: 3 R111(3,3) = 27
Uwagi
Należy zwrócić uwagę, że w żadnym z rozmieszczeń kolejność (układ) kul nie jest brany pod uwagę. Kule są po prostu wrzucane 'na kupkę’.
Wraz ze wzrostem wartości k i n obliczane wartości rosną.
Przykład 1
Gdy obliczymy dla k=2, n=10 każdą z ośmiu wartości R to zobaczymy, że wartości te stopniowo rosną, w takiej kolejności w jakiej umieściliśmy je w tabelce.
Wynik:
r000(10,2) = 5 r001(10,2) = 6 r010(10,2) = 9 r011(10,2) = 11 r100(10,2) = 511 r101(10,2) = 512 r110(10,2) = 1022 r111(10,2) = 1024
Przykład 2
Gdy obliczymy dla k=3, n=10 każdą z ośmiu wartości R to zobaczymy, że wartości te stopniowo rosną, w takiej kolejności w jakiej umieściliśmy je w tabelce.
Wynik:
r000(10,3) = 8 r001(10,3) = 14 r010(10,3) = 36 r011(10,3) = 66 r100(10,3) = 9330 r101(10,3) = 9842 r110(10,3) = 55980 r111(10,3) = 59049
Przykład 3
Obliczenia dla dużych liczb powinno się wykonywać w wątku, aby Java nie wyrzucała wyjątku.
Obliczamy 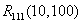
Wynik:
Start 10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 Koniec
Jest to liczba większa niż liczba atomów we Wszechświecie.
Przykład 4
Podobnie musimy mieć klasę do obliczania w wątku liczb Stirlinga II.
Obliczamy Stir2 dla n=50 i k=4.
Wynik:
Start 52818655359845224561907882505 Koniec
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

