
Kombinacje z powtórzeniami
Ogólny wzór to:
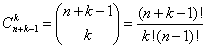
Mamy n-elementowy zbiór A. Mamy pewną liczbę k (k≤ n). Ze zbioru A wybieramy wszystkie k-elementowe podzbiory.
Zbiór A={a,b,c,d}. Wybieramy wszystkie 2-elementowe podzbiory zbioru:
(a,a), (a,b), (a,c), (a,d), (b,b), (b,c), (b,d), (c,c), (c,d), (d,d).
n=4, k=2
Jak widzimy uporządkowanie elementów nie gra roli. (a,b) = (b,a) i jest liczona tylko raz. Elementy mogą się powtarzać, czyli uwzględniamy pary typu (a,a). Mamy 10 wyników.
W naszym przykładzie:
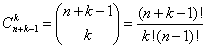
| a | b | c | d | |
|---|---|---|---|---|
| a | aa | ab | ac | ad |
| b | – | bb | bc | bd |
| c | – | – | cc | cd |
| d | – | – | – | dd |
Sprawdzamy:
n: 4 k: 2 kzp(4,2): 10
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

