
'Dzielenie' macierzy (Java)
Dzielenia macierzy nie definiuje się. W przypadku konieczności dzielenia zastępuje się je mnożeniem przez odwrotność. Np. dzielenie przez 2 jest równoznaczne z mnożeniem przez ![]() , gdyż 2×
, gdyż 2×![]() = 1, czyli
= 1, czyli
2×2-1 = 1.
Poniżej pokazuję jak wykorzystać 'dzielenie’ macierzy.
Rozwiązanie prostego równania
Mamy układ 2 równań z dwiema niewiadomymi:
3x + 2y = 17
5x – 3y = 3
Możemy to równanie zapisać w postaci macierzowej (można by to przedstawić za pomocą macierzy 2×2, ale z pewnych względów, o których powiem później, przedstawiam zagadnienie w postaci macierzy 3×3):
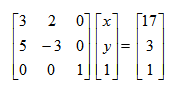
Żeby uzyskać wynik musimy podzielić obie strony równania przez macierz stojącą po lewej stronie. Ponieważ dzielenie nie jest określone pomnożymy obie strony przez odwrotność tej macierzy:
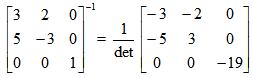
Ponieważ det = -19 ≠ 0 równanie ma rozwiązanie.
Po pomnożeniu mamy:
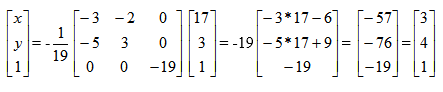
Nasze równanie ma rozwiązanie: x = 3, y = 4.
Możemy to też zapisać:
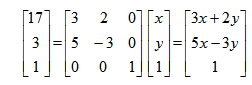
Geometrycznie rzecz biorąc punkt P(3,4) jest punktem przecięcia się obu linii (Matrix037):
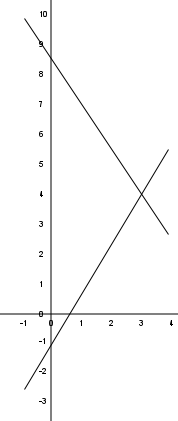
Nasz punkt P(x, y) = P(3, 4) został transformowany na punkt P(17, 3). Znając wynik transformacji P(17, 3) możemy, jak widzimy powyżej, znaleźć punkt transformowany. Znając punkt transformowany możemy znaleźć punkt wyjściowy transformacji.
Pliki do ściągnięcia
Moduł matrices – aktualny stan projektu = 015;

