
Ułamki i rozwinięcia dziesiętne
Ułamkiem dziesiętnym nazywamy ułamek, którego mianownik jest potęgą liczby 10.
Rozwinięciem dziesiętnym liczby rzeczywistej nazywamy przedstawienie jej w ciągu:
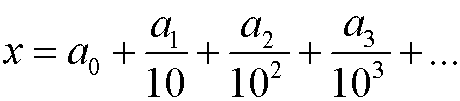
gdzie a0 to dowolna liczba całkowita, a pozostałe liczby indeksowane to liczby całkowite w przedziale zamkniętym<0, 9>.
Rozwinięcie dziesiętne symbolicznie zapisywane jest jako a0,a1a2a3
Właściwości rozwinięć dziesiętnych
Gdy wykonamy dzielenie licznika przez mianownik otrzymamy rozwinięcie dziesiętne tego ułamka. Są trzy możliwości.
1. Rozwinięcie nieskończone i nieokresowe
Dzieje się tak, gdy wynikiem jest liczba niewymierna np. (obwód koła)/(średnicę koła) = Π
2. Rozwinięcie skończone
Rozwinięcie ułamka jest skończone wtedy i tylko wtedy, gdy po skróceniu ma postać
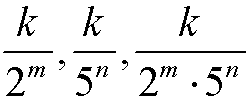
gdzie k jest liczbą całkowitą, a m i n są liczbami naturalnymi.
np: 2/5 = 0,4
3. Rozwinięcie nieskończone okresowe
Rozwinięcie dziesiętne nieskończone nazywamy okresowym, gdy od pewnego miejsca w rozwinięciu, grupa cyfr zaczyna się powtarzać.
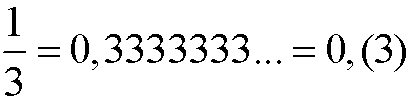
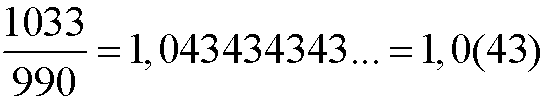
Cyfry okresu umieszczone są w nawiasach.

