
Permutacje z powtórzeniami
Mamy zbiór n-elementowy. Szukamy wszystkich możliwych ustawień n-elementów. Elementy mogą się powtarzać.
Wzór ogólny:
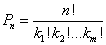
gdzie
n – liczba elementów
k1…km – liczba powtórzeń każdego elementu
Przykład 1
tata ={t,a,t,a}
(a,a,t,t),(a,t,a,t),(a,t,t,a),(t,a,a,t),(t,a,t,a),(t,t,a,a)
Mamy 6 możliwości.
n=4
kt=2 (element t powtarza się 2 razy)
ka =2 (element a powtarza się dwa razy)
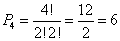
Sprawdzamy
n: 4
[2, 2]
pzp(4){2,2}= 6
Przykład 2
tama ={t,a,m,a}
(t,a,m,a)(a,m,a,t)(m,a,t,a)
(t,a,a,m)(a,m,t,a)(m,a,a,t)
(t,m,a,a)(a,t,m,a)(m,t,a,a)
(a,t,a,m)
(a,a,t,m)
(a,a,m,t)
n=4
kt=1
ka=2
km=1
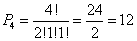
Sprawdzamy
n: 4
[1, 2, 1]
pzp(4){1,2,1}= 12
Kody
Kody do obliczeń w języku JavaScript możesz znaleźć w książce Matematyka dla programistów JavaScript.
Kody do obliczeń w języku Java możesz znaleźć w książce Matematyka dla programistów Java.

