
Wyznacznik macierzy (Java) (1)
Wyznaczniki obliczane są dla macierzy kwadratowych. Wyznacznik oznaczany jest jako ![]() albo |A|.
albo |A|.
Inwersja
Mamy skończony ciąg liczb rzeczywistych ![]() , np.
, np. ![]()
Para liczb ![]() tworzy inwersję jeśli
tworzy inwersję jeśli ![]() oraz
oraz ![]() . Liczby 5 i 4 w naszym ciągu tworzą inwersję, gdyż
. Liczby 5 i 4 w naszym ciągu tworzą inwersję, gdyż ![]() .
.
Permutacje bez powtórzeń
Mamy zbiór n-elementowy. Szukamy wszystkich możliwych ustawień n-elementów. Dany element się nie powtarza.
Wzór ogólny to:
![]()
Dla trzech elementów mamy 6 możliwych ustawień.
A={a,b,c}
(a,b,c) – 0 inwersji
(a,c,b) – 1 inwersja
(b,a,c) – 1 inwersja
(b,c,a) – 2 inwersje
(c,a,b) – 2 inwersje
(c,b,a)- 3 inwersje
Definicja wyznacznika macierzy
Wyznacznik macierzy jest liczbą przyporządkowaną macierzy w następujący sposób:
![]()
gdzie
![]() jest permutacją zbioru
jest permutacją zbioru ![]()
![]() jest liczbą inwersji w permutacji
jest liczbą inwersji w permutacji ![]()
Wyznacznik macierzy
![]()
Mamy 1 element ![]()
Mamy 1 permutację ![]()
![]() – 0 inwersji, czyli
– 0 inwersji, czyli ![]()
Dla macierzy ![]() wyznacznik wynosi
wyznacznik wynosi
![]() , czyli
, czyli
![]()
Czyli wyznacznik macierzy ![]() jest obliczany następująco:
jest obliczany następująco:
![]()
Wyznacznik macierzy 2 × 2
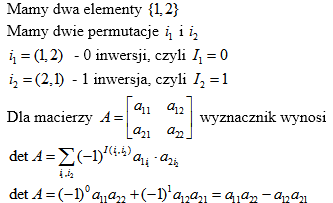
Czyli wyznacznik macierzy 2 × 2 jest obliczany następująco:
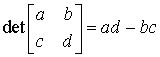
Wyznacznik macierzy 3 × 3

Jest to tzw. metoda Sarrusa.
W skrócie:
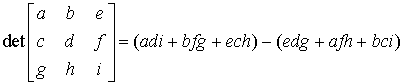
Np. 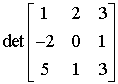 = (0 + 10 – 6) – (0 + 1 -12) = 4 – (-11)= 4 + 11 = 15
= (0 + 10 – 6) – (0 + 1 -12) = 4 – (-11)= 4 + 11 = 15
Jeśli będziemy mieli do czynienia z macierzą transformacji:
det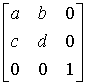 = (ad1 + 000 + 0c0) – (0d0 + a00h + bc1) = ad – bc
= (ad1 + 000 + 0c0) – (0d0 + a00h + bc1) = ad – bc
a w innym przypadku:
det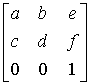 = (ad1 + bf0 + ec0) – (ed0 + af0 + bc1) = ad1 -bc1 = ad – bc
= (ad1 + bf0 + ec0) – (ed0 + af0 + bc1) = ad1 -bc1 = ad – bc

